Examinons ce qui se passe lorsque des valeurs négatives apparaissent sous le symbole du radical (comme radicande) pour les racines cubiques et les racines carrées.
Dans certaines situations, les nombres négatifs sous un symbole de radical sont OK. Par exemple, 
n’est pas un problème puisque (-2) – (-2) – (-2) = -8, ce qui fait que la réponse est -2. Dans les problèmes de racines cubiques, il est possible de multiplier une valeur négative par elle-même trois fois et d’obtenir une réponse négative.
Des difficultés apparaissent cependant lorsqu’on examine un problème tel que 
. Ce problème de racine carrée demande un nombre multiplié par lui-même qui donnera un produit (réponse) de -16. Il n’y a tout simplement aucun moyen de multiplier un nombre par lui-même et d’obtenir un résultat négatif. Considérez : (4) – (4) = 16 et (-4) – (-4) = 16.
|
ROOTS DU CUBE:
 |
Mais
|
ROOTS DU CARRE:
 |
|
Oui, (-2) x (-2) x (-2) = -8.
Pas de problème. |
Nope ! (4) x (4) ≠ -16. |
Les racines carrées sont les coupables ! Les difficultés surviennent lorsqu’on rencontre une valeur négative sous une racine carrée. Il n’est pas possible de mettre une valeur au carré (la multiplier par elle-même) et d’arriver à une valeur négative. Alors, que fait-on ?
 |
La racine carrée d’un nombre négatif n’existe pas parmi l’ensemble des Nombres Réels.
|
Lorsque les problèmes de négatifs sous une racine carrée sont apparus, les mathématiciens pensaient qu’une solution n’existait pas. Ils voyaient des équations telles que x2 + 1 = 0, et se demandaient ce que la solution 
signifiait vraiment.
Pour tenter de résoudre ce problème, les mathématiciens ont « créé » un nouveau nombre, i, que l’on appelait « nombre imaginaire », puisqu’il ne faisait pas partie de l’ensemble des « nombres réels ». Ce nouveau nombre a été considéré avec beaucoup de scepticisme. Le nombre imaginaire est apparu pour la première fois sous forme imprimée en l’an 1545.
 |
Le nombre imaginaire « i » est la racine carrée du un négatif. |
Un nombre imaginaire possède la propriété unique que lorsqu’il est élevé au carré, le résultat est négatif.
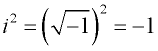
Considérez : 
Le processus de simplification d’un radical contenant un facteur négatif est le même que la simplification normale des radicaux. La seule différence est que le 
sera remplacé par un « i « .
Au fur et à mesure que la recherche sur les nombres imaginaires se poursuivait, on a découvert qu’ils comblaient en fait une lacune dans les mathématiques et servaient un objectif utile. Les nombres imaginaires sont essentiels à l’étude de sciences telles que l’électricité, la mécanique quantique, l’analyse des vibrations et la cartographie.
Lorsque le i imaginaire a été combiné avec l’ensemble des nombres réels, l’ensemble englobant des nombres complexes a été formé.
.
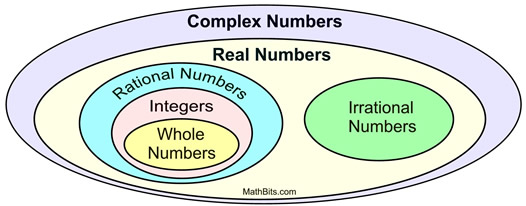