Frecuencia y tono

¿Qué es la frecuencia? La frecuencia es «la frecuencia» de algo. Dado que el sonido son vibraciones, utilizamos la frecuencia para describir la frecuencia con la que vibra algo.La frecuencia se mide en Hertz (Hz), que es simplemente «la frecuencia por segundo».Así, algo que oscila a 1 Hz está vibrando una vez por segundo. Una vibración «completa» se llama «ciclo», y se mide en un pico y un valle completos de una onda (es decir, la distancia máxima o «amplitud» por encima del punto medio o «0», representado en el eje x). (En los primeros tiempos de la música electrónica, se utilizaban los términos «ciclos por segundo» en lugar de Hz, que puede ver en muchos sintetizadores antiguos/antiguos hoy en día).

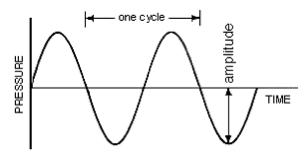
La imagen de arriba es una onda sinusoidal–la representación más pura de una sola frecuencia o vibración. El tiempo que tarda la onda en completar un ciclo es la frecuencia de la onda (de nuevo, «la frecuencia» con la que vibra). Más vibraciones por segundo (es decir, oscilaciones más rápidas) producen frecuencias de sonido «más altas» y menos vibraciones por segundo (es decir, oscilaciones más lentas) producen frecuencias de sonido «más bajas». El ser humano sólo puede oír frecuencias comprendidas entre 20Hz y 20.000Hz (20kHz) (para más información, véase https://en.wikipedia.org/wiki/Hearing_range).

En la música, los términos frecuencia, tono y timbre están relacionados.Un tono es un sonido con una o más frecuencias identificables. La frecuencia es la medida empírica de un fenómeno físico, definida como los ciclos (de vibración) por segundo. El tono es una percepción subjetiva de la altura relativa de un tono, como «alto» o «bajo» (para más información, véase Conceptual Modelsand Cross-Domain Mapping de Lawerence Zbikowskihttp://zbikowski.uchicago.edu/pdfs/ZbikowskiConceptualmodels_1997.pdf).

Mientras que las frecuencias se representan con números (Hz), el tono se representa con letras. Por ejemplo, si alguna vez has oído a una orquesta «afinar» al principio de un concierto, un solo intérprete (normalmente un oboe o un violín) toca un «la» que se mide a 440 Hz (denominado A440). En cuanto a la afinación, sólo utilizamos las letras A, B, C, D, E, F y G (se utilizan símbolos adicionales para subirlas o bajarlas, más adelante). Estos tonos se repiten cada 8 notas, lo que se llama una octava. Para diferenciar a qué octavas nos referimos cuando hablamos de tono, se añade un número después de la letra. Por ejemplo, A440 (Hz) se llama A4 en términos de tono. Pero no te confundas, el 4 se refiere a la octava en la que nos referimos a ese La en particular (específicamente en el piano); es sólo una coincidencia que la frecuencia sea 440, el 4 no se refiere específicamente a eso. Pero por qué entonces A4 es 440 Hz, se preguntará usted… bueno, hay una respuesta bastante complicada a esa pregunta, pero en última instancia es efectivamente arbitraria. En pocas palabras, un grupo de personas se reunió en el siglo XIX y decidió que era así. (Si quiere saber más sobre el tema, investigue en A440 o en las normas de afinaciónhttps://en.wikipedia.org/wiki/A440(pitchstandard)).

Es importante tener en cuenta que la frecuencia es absoluta, mientras que el tono es relativo (estos cambios relativos se denominan «afinación»). Utilizamos los tonos para describir su relación (es decir, la relación) con otros tonos y el análisis de esas relaciones es la base de la ‘teoría musical’. En general, hemos acordado que A4 se define como el tono cuya frecuencia es de 440 Hz (una referencia absoluta). A continuación, podemos determinar el «tono» o la «afinación» de todas las demás notas en relación con eso utilizando una fórmula de afinación particular.

Un aspecto muy importante de toda la teoría de la música es que las octavas se definen específicamente como «duplicar» o «reducir a la mitad» la frecuencia de un tono. Por ejemplo, las frecuencias 220 Hz, 440 Hz y 880 Hz son todas A, pero existen en diferentes octavas: A3, A4 y A5 respectivamente. En la teoría musical occidental, hemos acordado generalmente (y francamente, de forma arbitraria) que dentro de cada octava hay 12 subdivisiones o tonos iguales. Entonces, ¿cómo determinamos dónde están «afinadas» esas otras notas en relación con esa A440? Bueno, después de muchos años de experimentación se decidió que la siguiente fórmula determina la relación relativa entre los tonos (más específicamente, la frecuencia f de la enésima tecla de un piano estándar):

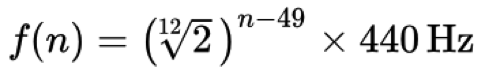https://en.wikipedia.org/wiki/Pianokeyfrequencies

En pocas palabras, cada tono/tono en la afinación de la música clásica occidental se deriva comenzando con A440 como «tono de referencia» y luego multiplicando o dividiendo por la raíz duodécima de dos (~1,059463) para llegar a otro tono por encima o por debajo de ese tono de referencia. El número 49 en este caso es arbitrario (A4 es la tecla 49 en un teclado de piano estándar) y en la música por ordenador solemos utilizar números MIDI para nuestros cálculos -A440 es la tecla MIDI número 69, por ejemplo (más información sobre los estándares MIDI en otra lección).

Hay que tener en cuenta que esta fórmula representa sólo un estilo particular de «afinación» que existe dentro de la tradición de la música clásica occidental y se utiliza en general como el «estándar mundial» cuando se habla de las relaciones de tono / frecuencia / tono en general, a pesar de que estas relaciones son arbitrarias y existen otros sistemas de afinación dentro de las diferentes culturas y tradiciones.Este sistema conserva una «regla» importante que las octavas se definen como el doble o la reducción exacta de las frecuencias, manteniendo las mismas relaciones (de tono) de dividir cada octava en 12 partes iguales. Llamamos a este sistema de afinación 12 tonos iguales y sirve de base para la mayor parte del mundo como sistema de afinación fundamental y consensuado, especialmente cuando se trata de la estandarización de equipos musicales electrónicos. (Todos los pianos se afinan en este sistema y todos los datos MIDI siguen este principio general).

En la terminología musical, describimos los tonos (o tonos) como ascendentes o descendentes en términos de «pasos». Hay dos tipos de pasos: medios pasos y pasos enteros (también llamados semitonos o tonos enteros). El aumento de las notas en un medio paso (es decir, un semitono) se indica con un símbolo ♯ llamado «sostenido» (número o símbolo de etiqueta) y el descenso de los tonos en un medio paso se indica con un símbolo ♭ llamado «bemol» (también se utiliza con frecuencia una «b» minúscula). Se puede pensar en los semitonos o medios pasos como la distancia mínima entre dos teclas de piano o trastes de guitarra adyacentes.

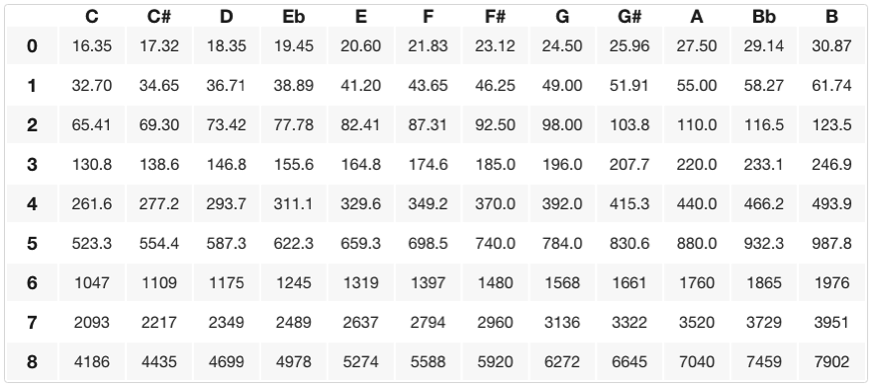
Para obtener la frecuencia de un semitono más arriba de A4 multiplicamos 440 Hz por la duodécima raíz de dos para obtener ~466,2 Hz, lo que nos da un A# (o Bb). El A# y el Bb se denominan «notas enarmónicas», o tonos que son técnicamente la misma frecuencia pero que podrían «escribirse» de forma diferente dependiendo de la «clave» o del contexto musical del que estemos hablando (más sobre esto en otra lección). Para obtener la frecuencia de un paso entero desde A4, podemos multiplicar 440Hz dos veces por la duodécima raíz de dos, lo que nos da ~493,9 Hz o B4. A continuación se muestra una tabla de todas las frecuencias específicas con su relación tono/octava (los nombres de las notas están en el eje de las abscisas y los números de las octavas están en el eje de las ordenadas).

https://www.seventhstring.com/resources/notefrequencies.html

Esta colección de ‘doce notas por octava’ se llama escala cromática.Una ‘escala’ es una colección de notas en orden ascendente/descendente que comienza/termina en una frecuencia o tono fundamental. Una escala cromática comienza en cualquier tono y asciende (o desciende) en 11 medios pasos (semitonos) adyacentes desde su fundamental. En el gráfico anterior, puede encontrar las frecuencias o notas/pitches específicas de cualquier escala cromática comenzando en una nota determinada (la fundamental) y contando hacia arriba o hacia abajo 11 semitonos (tonos adyacentes).

Si se ha dado cuenta, algunas de las notas en el gráfico anterior se «deletrean» con un # (sostenido) mientras que otras se deletrean con un b (bemol). Teóricamente, cualquier nota puede subir o bajar medio paso o un tono entero añadiendo uno de estos símbolos después de ella. Sin embargo, hay convenciones para que ciertas notas se «deletreen» de una manera particular, dada la prevalencia y la previsibilidad de las prácticas de la teoría musical occidental. En lo que respecta a las «grafías enarmónicas» de las notas y los tonos (notas con la misma frecuencia pero representadas como tonos diferentes), la tabla anterior representa las grafías más comunes de las notas y los tonos con respecto a las prácticas tradicionales de las «firmas de clave» en la música, pero no incluye todas las posibilidades. Las siguientes notas son deletreos enarmónicos comunes (las barras inclinadas indican que las notas/tonos tienen la misma frecuencia pero pueden representarse o «deletrearse» como tonos diferentes):

C#/Db D#/Eb F#/Gb G#/Ab A#/Bb

Por supuesto, teóricamente cualquier nota se puede subir o bajar un medio paso (semitono) o incluso un paso entero (tono entero) con un símbolo # o b y algo de teoría musical más avanzada entra en lo que se llama dobles bemoles y -subidas.Sin complicarse demasiado o profundizar en ello, todas las escalas o claves musicales son una colección de medios pasos y pasos enteros y la ortografía de esos tonos da al intérprete pistas sobre las relaciones (es decir, proporciones) entre los tonos que el compositor está utilizando.

• Hertz (Hz)
• Frecuencia
• Tono
• Tono
• A4 (A440)
• Octavas
• Pasos enteros (tonos enteros)
• Medios pasos (semitonos)

Self-Quiz

• El tono G3 tiene una frecuencia fundamental de 196Hz. Sin consultar una tabla, ¿cuáles son las frecuencias de los tonos G2 y G4 (una octava por debajo y por encima de G4)?

Recursos adicionales