Euler azonossága a matematikában található egyenlőség, amelyet egy Shakespeare-szonetthez hasonlítottak, és “a legszebb egyenletként” jellemeztek. Ez egy speciális esete a komplex aritmetika egyik alapegyenletének, az Euler-formulának, amelyet a néhai nagy fizikus, Richard Feynman előadásaiban “a mi ékszerünknek” és “a matematika legcsodálatosabb képletének” nevezett.
A BBC-nek adott interjúban David Percy professzor, a Matematika és Alkalmazásai Intézetének munkatársa azt mondta, hogy az Euler-azonosság “igazi klasszikus, ennél jobbat nem lehet találni… Egyszerű ránézni, mégis hihetetlenül mélyreható, az öt legfontosabb matematikai állandót tartalmazza.”
Euler azonossága egyszerűen így írható: eiπ + 1 = 0
Az öt állandó a következő:
- A 0.
- A 1.
- A π szám, egy irracionális szám (végtelen számjegyekkel), amely a kör kerületének és átmérőjének aránya. Ez körülbelül 3,14159…
- Az e szám, szintén irracionális szám. A természetes logaritmusok alapja, amely a kamatos kamat és a számtan tanulmányozása során természetesen keletkezik. Az e szám áthatja a matematikát, látszólag a semmiből bukkan fel rengeteg fontos egyenletben. Körülbelül 2,71828….
- az i szám, amelyet a negatív egy négyzetgyökeként definiálnak: √(-1). A képzeletbeli számok legalapvetőbbike, azért nevezik így, mert a valóságban egyetlen számot sem lehet önmagával megszorozni, hogy negatív számot kapjunk (és ezért a negatív számoknak nincs valós négyzetgyökük). A matematikában azonban sok olyan helyzet van, amikor kénytelenek vagyunk a negatív számok négyzetgyökét venni. Az i betűt ezért egyfajta helyettesítő betűként használják az olyan helyek jelölésére, ahol ez megtörtént.
Jelentős matematikus
Leonhard Euler 18. századi svájci születésű matematikus volt, aki számos olyan fogalmat dolgozott ki, amelyek a modern matematika szerves részét képezik. Pályafutása nagy részét az oroszországi Szentpéterváron töltötte. Az Amerikai Haditengerészeti Akadémia (USNA) szerint minden idők egyik legtermékenyebb matematikusa volt, 886 publikációja és könyve jelent meg. Termésének nagy része élete utolsó két évtizedében született, amikor teljesen vak volt. Annyi munkája volt, hogy a Szentpétervári Akadémia több mint 30 éven át folytatta munkásságának posztumusz kiadását.
Euler fontos hozzájárulásai közé tartozik az Euler-képlet és az Euler-tétel, mindkettő a kontextustól függően különböző dolgokat jelenthet. Az USNA szerint a mechanikában vannak “Euler-szögek (egy merev test orientációjának megadására), Euler tétele (hogy minden forgásnak van egy tengelye), Euler egyenletei a folyadékok mozgására és az Euler-Lagrange-egyenlet (amely a variációszámításból származik).”
Komplex számok szorzása
Euler azonossága természetesen a komplex számok kölcsönhatásaiból ered, amelyek olyan számok, amelyek két darabból állnak: egy valós számból és egy képzeletbeli számból; egy példa erre a 4+3i. A komplex számok számos alkalmazásban megjelennek, például a hullámmechanikában (a kvantummechanikán belüli tanulmány) és a váltakozó áramot használó áramkörök tervezésében (az elektrotechnikában gyakori gyakorlat). Ezenkívül a komplex számok (és rokonaik, a hiperkomplex számok) rendelkeznek egy olyan tulajdonsággal, amely különösen hasznossá teszi őket a számítógépes grafika, a robotika, a navigáció, a repülésdinamika és a pályamechanika tanulmányozásában: összeszorzásuk hatására elfordulnak. Ez a tulajdonság segít megérteni az Euler-identitás mögött álló okfejtést.
A lenti példában öt komplex számot ábrázolunk a komplex síkon, és ezek együtt egy “ház alakot” alkotnak. A komplex sík hasonló a számegyeneshez, azzal a különbséggel, hogy kétdimenziós. A vízszintes irány a valós számokat, a függőleges tengely pedig a képzeletbeli számokat jelöli. Minden ház alakú komplex számot megszorozunk a 4+3i komplex számmal, és újra felrajzoljuk (zöld nyíl).
Amint látható, a 4+3i-vel való szorzás azt eredményezi, hogy a ház alakja tágul (növekszik a területe és ugyanannyival távolodik a 0+0i origótól) és forog (bizonyos szöggel megdől). Hogy megmutassuk, hogy pontosan ez a 4+3i-vel való szorzás hatása, a ház ötszörös nagyításának és 36,9 fokos elforgatásának hatása is látható (piros nyíl). Pontosan ugyanez a hatás jön létre.
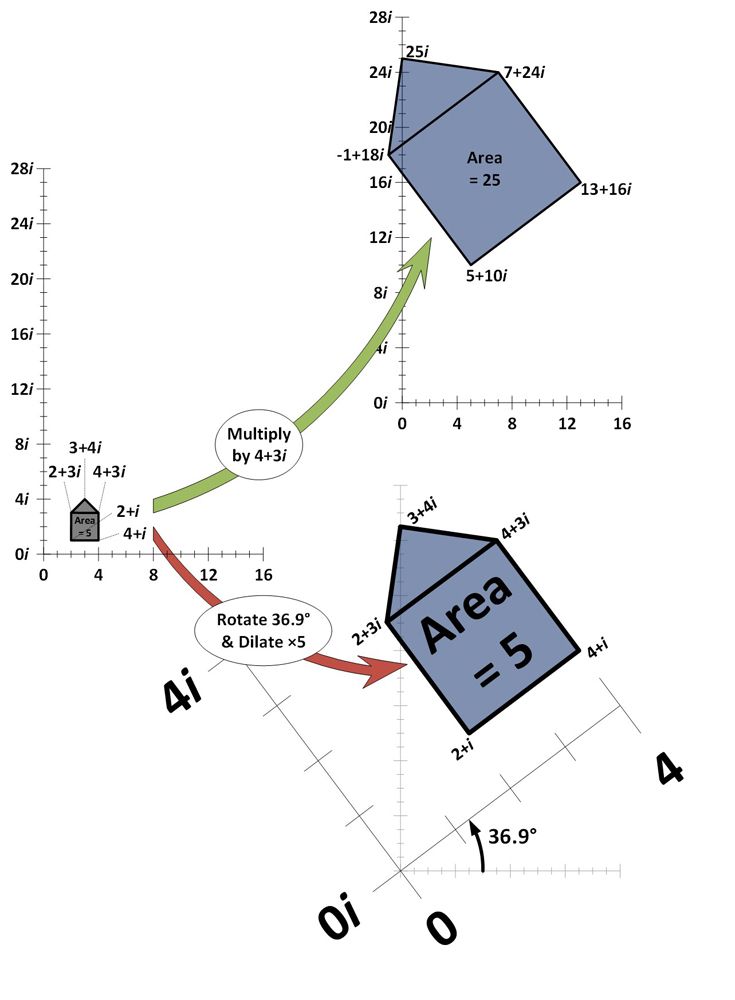
A komplex sík bármely számmal való szorzásának hatását különböző mértékű tágítással és elforgatással lehet előidézni.
A komplex számok poláris alakja
A forgatás és a tágítás mértékét a 4+3i számban rejlő tulajdonságok határozzák meg, amely, mint az alábbi ábrán látható, öt egységre van az origótól (r = 5), és 36,9 fokos szöget zár be a vízszintes tengellyel (φ = 36,9°). Ezeket a méréseket az úgynevezett komplex szám poláris alakjában (reiφ) használjuk, szemben a szokásos négyszögletes alakkal (a+bi).
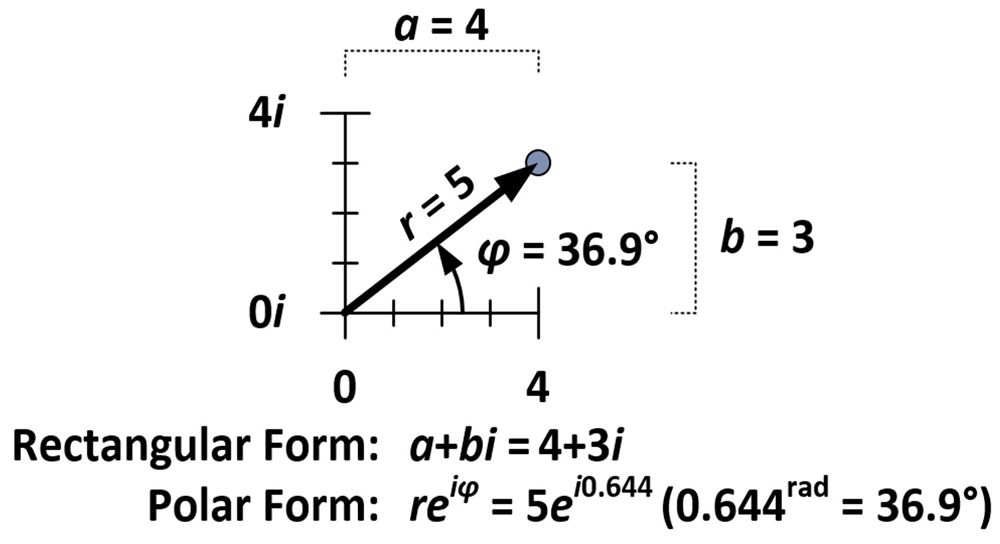
A poláris forma megköveteli, hogy φ-et radiánban mérjük. Egy radián (1rad) körülbelül 57,3 fok; ez annak a szögnek a mértéke, amelyet akkor képezünk, ha egy kör sugarát a kör kerületéhez tekerjük. A π radián mértéke egy kör felét, a 2π radián mértéke pedig egy teljes kört ölel fel.
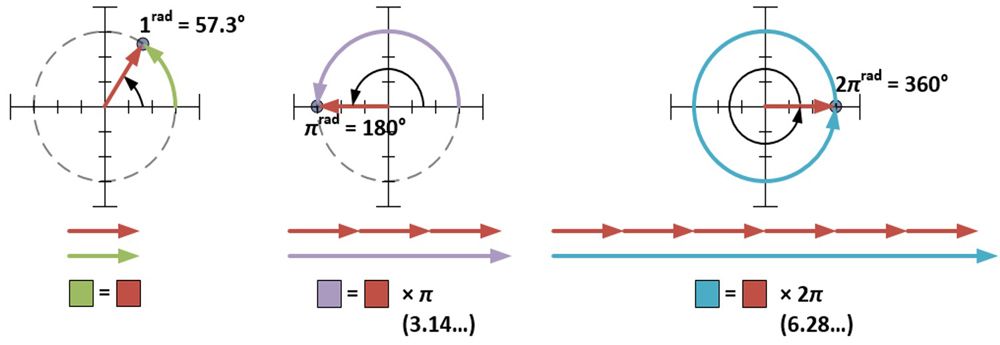
A 4+3i szögmértéke 0,644 radián (36,9° = 0,644rad), vagyis a 4+3i poláris alakja 5ei0,644. Az r és φ méretei is meghatározhatók az egyes ház-alakú pontokhoz, és a 4+3i-vel való szorzás tágító/forgató hatásának elérésének egy másik módja, ha minden r-t megszorozunk öttel, és minden φ-hez hozzáadunk 36,9 fokot (vagy 0,644radot). Ebből a szemléltetésből láthatjuk, hogy amikor a komplex számokat összeszorozzuk, a távolságok megsokszorozódnak, a szögek pedig összeadódnak. Ez egy, az exponenseknek saját tulajdonsága miatt van így, ami algebrailag is kimutatható.
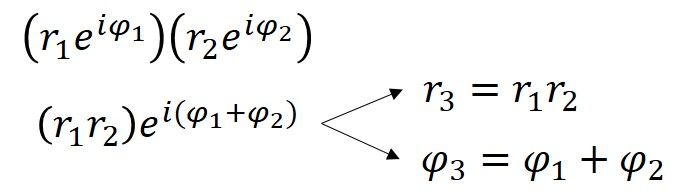
A komplex számok poláris alakjának megállapításával az Euler-identitás kérdése csupán az a+bi speciális esete a = -1 és b = 0 esetén. Következésképpen a reiφ poláris alakra ez r= 1 és φ = π (mivel πrad = 180°).
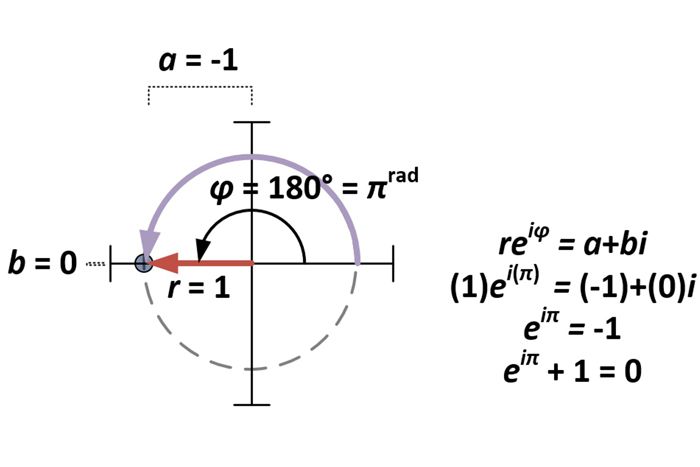
A polárforma levezetése
A komplex számok polárformájából következik ugyan az Euler-identitás, de a polárforma levezetése (különösen az e szám spontán megjelenése) számtan nélkül nem lehetséges.
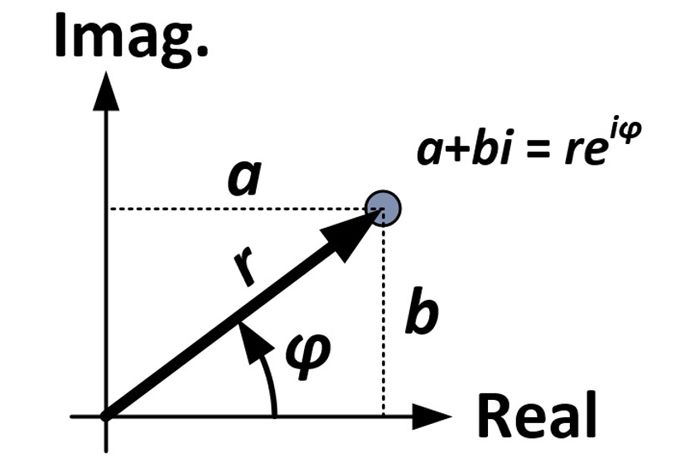
Kezdjük a komplex szám négyszögletes formájával:
a + bi
A diagramból és a trigonometriából a következő helyettesítéseket tudjuk elvégezni:
(r-cosφ) + (r-sinφ)i
Ezért r-t faktorálhatjuk:
r-(cosφ + i-sinφ)
A “cosφ + i-sinφ”-t néha cisφ-nek nevezik, ami a koszinusz plusz képzetes szinusz rövidítése.”
r-cisφ
A cisφ függvényről kiderül, hogy egyenlő eiφ-vel. Ez az a rész, amit számítás nélkül lehetetlen megmutatni. Az alábbiakban két levezetés látható:

Az r-cisφ egyenletet tehát r-eiφ szabványos poláris formában írjuk fel.