Vizsgáljuk meg, mi történik, ha negatív értékek jelennek meg a gyökszimbólum (mint radikális) alatt a kockagyök és a négyzetgyök esetében.
Némely helyzetben a negatív számok a gyökszimbólum alatt rendben vannak. Például a 
nem jelent problémát, mivel (-2) – (-2) – (-2) – (-2) = -8, így a válasz -2. A kockagyök problémákban lehetséges, hogy egy negatív értéket háromszor megszorozzuk önmagával, és negatív választ kapunk.
Nehézségek azonban akkor merülnek fel, amikor olyan feladatot vizsgálunk, mint a 
. Ez a négyzetgyökfeladat olyan számot kérdez, amelyet önmagával megszorozva -16-os szorzatot (választ) kapunk. Egyszerűen nem lehet úgy megszorozni egy számot önmagával, hogy negatív eredményt kapjunk. Vegyük például: (4) – (4) = 16 és (-4) – (-4) = 16.
|
KUBUSZGYÖK:
 |
BUT
|
NÉGYSZÖK:
 |
|
Igen, (-2) x (-2) x (-2) = -8.
Nem probléma. |
Nope! (4) x (4) ≠ -16. |
A négyzetgyök a bűnös! A nehézségek akkor merülnek fel, amikor egy négyzetgyök alatt negatív értékkel találkozunk. Nem lehet úgy négyzetgyököt képezni (megszorozni önmagával), hogy negatív értéket kapjunk. Mit tegyünk tehát?
 |
Negatív szám négyzetgyöke nem létezik a valós számok halmazában.
|
Amikor először jelentek meg a négyzetgyök alatti negatívokkal kapcsolatos problémák, a matematikusok úgy gondolták, hogy nem létezik megoldás. Olyan egyenleteket láttak, mint például x2 + 1 = 0, és azon tűnődtek, hogy mit jelenthet valójában a 
megoldás.
A probléma megoldására a matematikusok “kreáltak” egy új számot, az i-t, amelyet “képzeletbeli számnak” neveztek, mivel nem szerepelt a “Valós számok” halmazában. Ezt az új számot sokan szkeptikusan szemlélték. A képzeletbeli szám először 1545-ben jelent meg nyomtatásban.
 |
A képzeletbeli szám “i” a negatív egy négyzetgyöke. |
A képzeletbeli számnak megvan az az egyedülálló tulajdonsága, hogy ha négyzetre tesszük, az eredmény negatív.
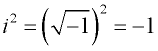
Gondoljuk meg: 
A negatív tényezőt tartalmazó gyök egyszerűsítésének folyamata megegyezik a normál gyök egyszerűsítésével. Az egyetlen különbség az, hogy a 
helyébe egy “i ” kerül.
Amint a képzeletbeli számokkal kapcsolatos kutatások folytatódtak, kiderült, hogy valójában egy űrt töltenek be a matematikában, és hasznos célt szolgálnak. A képzetes számok nélkülözhetetlenek az olyan tudományok tanulmányozásához, mint az elektromosság, a kvantummechanika, a rezgéselemzés és a térképészet.
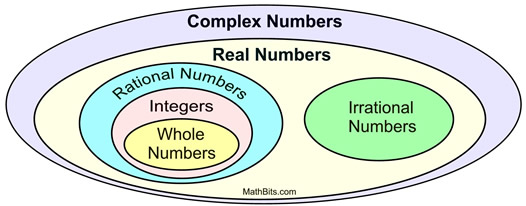
Amikor a képzetes i-t a valós számok halmazával kombinálták, létrejött a komplex számok mindent átfogó halmaza.
