Guardando la natura, potresti aver notato piante intricate come queste:


Questa felce consiste di molte piccole foglie che si diramano da una più grande.


Questo broccolo romanesco consiste di piccole conescubesspheres che girano a spirale attorno ad una più grande.
Inizialmente, queste appaiono come forme altamente complesse – ma quando si guarda più da vicino, si può notare che entrambe seguono un modello relativamente semplice: tutte le singole parti delle piante sembrano esattamente le stesse dell’intera pianta, solo più piccole. Lo stesso schema si ripete più e più volte, a scale più piccole.
In matematica, chiamiamo questa proprietà autosimilarità, e le forme che la possiedono sono chiamate frattali. Sono alcuni degli oggetti più belli e più bizzarri di tutta la matematica.
Per creare i nostri frattali, dobbiamo iniziare con un modello semplice e poi ripeterlo più e più volte, su scale più piccole.
Uno dei modelli più semplici potrebbe essere un segmento di linea, con altri due segmenti che si diramano da un’estremità. Se ripetiamo questo schema, entrambi questi segmenti blu avranno anche altri due rami alle loro estremità.
Puoi spostare i punti blu per cambiare la lunghezza e l’angolo di tutti i rami. Poi aumenta il numero di iterazioni usando il cursore qui sotto.
A seconda della posizione dei rami, puoi creare modelli completamente diversi – che assomigliano alla felce qui sopra, a un albero, o a pentagoni annidati. Cos’altro puoi trovare?
Un altro famoso frattale è il triangolo di Sierpinski. In questo caso, iniziamo con un grande triangolo equilatero, e poi tagliamo ripetutamente triangoli più piccoli dalle parti rimanenti.
Notate come la forma finale è composta da tre copie identiche di se stessa, e ognuna di queste è composta da copie ancora più piccole dell’intero triangolo! Potresti continuare ad ingrandire il triangolo per sempre, e i modelli e le forme continueranno sempre a ripetersi.
Le piante all’inizio di questo capitolo sembrano proprio dei frattali, ma è chiaramente impossibile creare veri frattali nella vita reale. Se continuiamo a ripetere lo stesso schema più e più volte, sempre più piccolo, alla fine arriveremmo a cellule, molecole o atomi che non possono più essere divisi.
Tuttavia, usando la matematica, possiamo pensare alle proprietà che i veri frattali “avrebbero” – e queste sono molto sorprendenti…
Dimensioni dei frattali
Prima, pensiamo alla dimensione dei frattali. Una linea ha dimensione . Quando la si scala di un fattore 2, la sua lunghezza aumenta di un fattore 21=2. Ovviamente!
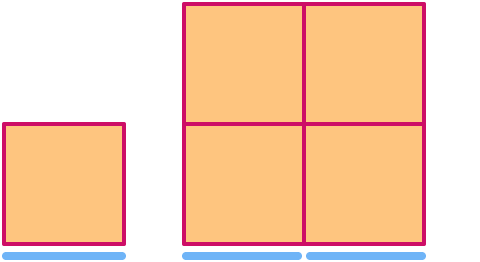
Un quadrato ha dimensione . Scalandolo di un fattore 2, la sua area aumenta di un fattore 22= .
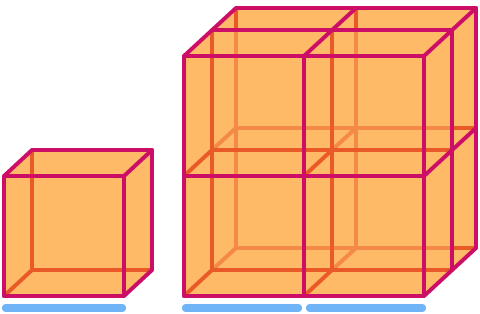
Un cubo ha dimensione . Quando lo si scala di un fattore 2, il suo volume aumenta di un fattore 23= . Notate che il cubo più grande nell’immagine consiste in 8 copie di quello più piccolo!
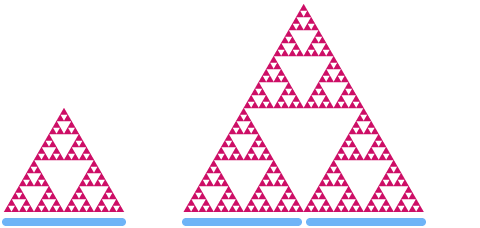
Ora diamo un’occhiata al triangolo di Sierpinski. Se lo scaliamo di un fattore 2, potete vedere che la sua “area” aumenta di un fattore di .
Diciamo che d è la dimensione del triangolo Sierpinski. Usando lo stesso schema di cui sopra, otteniamo 2d=3. In altre parole, d = log23log32 ≈ 1.585…
Ma aspetta… come può qualcosa avere una dimensione che non è un intero? Sembra impossibile, ma questa è solo una delle strane proprietà dei frattali. Infatti, questo è ciò che dà ai frattali il loro nome: hanno una dimensione frazionaria.
Con ogni iterazione, rimuoviamo una parte dell’area del triangolo di Sierpinski. Se potessimo farlo per un numero infinito di volte, in realtà non rimarrebbe alcuna area: ecco perché il triangolo di Sierpinski è qualcosa a metà tra un’area bidimensionale e una linea unidimensionale.
Mentre molti frattali sono autosimili, una definizione migliore è che i frattali sono forme che hanno una dimensione non intera.
Il fiocco di neve di Koch
In natura ci sono molte forme che sembrano frattali. Abbiamo già visto alcune piante all’inizio di questo capitolo. Altri grandi esempi sono i fiocchi di neve e i cristalli di ghiaccio:
Per creare il nostro fiocco di neve frattale, dobbiamo ancora una volta trovare una procedura semplice che possiamo applicare più volte.
Come il triangolo di Sierpinski, iniziamo con un singolo triangolo equilatero. Tuttavia, piuttosto che rimuovere triangoli più piccoli ad ogni passo, aggiungiamo triangoli più piccoli lungo il bordo. La lunghezza laterale di ogni triangolo è 131412 dei triangoli nel passo precedente.
La forma risultante è chiamata il fiocco di neve di Koch, dal nome del matematico svedese Helge von Koch. Notate, ancora una volta, che le piccole sezioni del bordo del fiocco di neve hanno esattamente lo stesso aspetto delle sezioni più grandi.
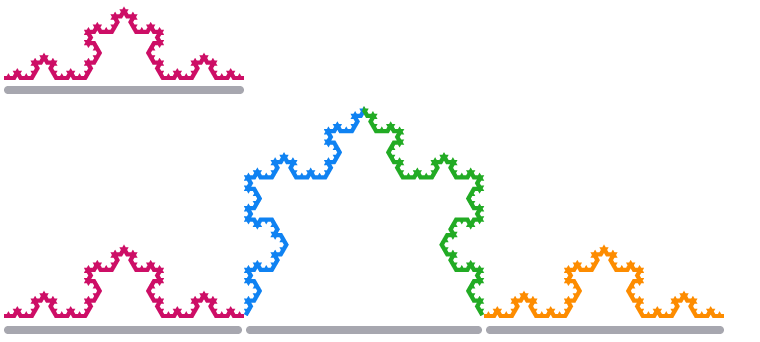
Quando scaliamo un segmento di bordo del Koch Snowflake di un fattore 3, la sua lunghezza quadrupla raddoppia.
Usando la stessa relazione tra dimensioni e fattori di scala di cui sopra, otteniamo l’equazione 3d=42d=42d=34d=3. Questo significa che la dimensione del fiocco di neve di Koch è d=log34≈1,262.
Area
Creare i fiocchi di neve di Koch è quasi come una sequenza ricorsiva: conosciamo la forma di partenza (un triangolo), e sappiamo come arrivare da un termine al successivo (aggiungendo altri triangoli su ogni bordo):


nuovi triangoli

nuovi triangoli

nuovi triangoli
Dopo la prima iterazione, il numero di nuovi triangoli aggiunti aumenta di un fattore di ad ogni passo. Allo stesso tempo, l’area di questi nuovi triangoli diminuisce di un fattore di ad ogni passo.
Diciamo che il primo triangolo ha un’area di 1. Allora l’area totale dei prossimi tre triangoli è 3×19=13. I passi successivi formano tutti una serie geometrica-serie aritmetica-serie quadratica, con rapporto comune 499443.
Usando la formula per la somma di serie geometriche infinite, possiamo calcolare che l’area totale del fiocco di neve Koch è
A=1+13×11-491+949-14=85=1.6.
Perimetro
Possiamo anche provare a calcolare il perimetro del fiocco di neve di Koch. Come abbiamo già visto prima, la lunghezza del perimetro cambia di un fattore 433414 ad ogni passo.
Questo significa che, ancora una volta, abbiamo una serie geometrica – ma in questo caso, non converge a 0non ha un primo termine. Questo significa che il perimetro del fiocco di neve Koch è in realtà infinitamente lungo!

Se questo sembra controintuitivo, basta ricordare che moltiplichiamo il perimetro per 43 ad ogni passo, e lo facciamo infinite volte.
È quasi impensabile che si possa avere una forma con un’area finita e anche una circonferenza infinita – ma questa è solo una delle tante proprietà inaspettate dei frattali.
Ti viene in mente qualche altro modo per creare i tuoi frattali?
“La mia anima sta spiraleggiando su frattali congelati tutto intorno…”
Spugna Menger
I frattali non devono essere “piatti”, come molti degli esempi sopra. Uno dei più famosi frattali che sembrano tridimensionali è la spugna di Menger, dal nome del matematico Karl Menger che la descrisse per la prima volta nel 1926.
Iniziamo con un cubo solido, e pratichiamo ripetutamente fori sempre più piccoli nei suoi lati. Ogni nuova iterazione di fori ha 131214 la larghezza della precedente iterazione di fori.
Un cubo 3×3×3 consiste di 27 cubi più piccoli, ma qui abbiamo rimosso alcuni di questi. La spugna di Menger consiste di copie di se stessa, che sono 3 volte più piccole.
Ora possiamo provare a calcolare la dimensione d della spugna di Menger proprio come abbiamo fatto per il fiocco di neve di Koch sopra. In questo caso otteniamo 3d=20, o d=log320≈2.727.
Se immaginate di ritagliare sempre più buchi, infinite volte, non ci sarebbe più alcun volume effettivo. Ecco perché il cubo è “non proprio” tridimensionale!
Coste frattali
Una delle caratteristiche chiave di tutti i frattali che abbiamo visto finora è che si può “zoomare” all’infinito e trovare sempre nuovi modelli. Intorno al 1920, il matematico britannico Lewis Fry Richardson si rese conto che lo stesso è vero per il confine o la linea costiera di molti paesi.
Si comincia con la forma di base del paese e, man mano che si ingrandisce, si aggiungono insenature di fiumi, baie ed estuari, poi singole scogliere, rocce, ciottoli e così via:
Questo è un problema significativo quando si cerca di calcolare la lunghezza del confine di un paese – come si decide quanto ingrandire e quali angoli e fessure includere?
Un modo per misurare la lunghezza della costa della Gran Bretagna, ad esempio, è quello di prendere un lungo righello, camminare intorno alle sue spiagge, e poi sommare tutte le distanze.
Se il righello è lungo ${rulers} km, dobbiamo usarlo ${count} volte, quindi otteniamo una linea costiera totale di ${count} × ${rulers} = ${count * rulers}km.
Possiamo continuare, con righelli sempre più piccoli, e ogni volta il nostro risultato per la lunghezza della linea di costa diventerebbe un po’ più lungo. Proprio come il fiocco di neve di Koch prima, sembra che la linea costiera della Gran Bretagna sia infinitamente lunga! Questo è spesso chiamato il paradosso della linea costiera.
Alcuni decenni dopo, il matematico Benoit Mandelbrot si imbatté nel lavoro di Richardson in un libro di biblioteca scartato, mentre lavorava all’IBM. Ne riconobbe l’importanza, e anche il modo in cui si collega alle ricerche più recenti sui frattali e le dimensioni.
La linea costiera della Gran Bretagna certamente “sembra” frattale, ma non è autosimile, come altri frattali che abbiamo visto prima. Per trovare la sua dimensione, possiamo disegnarla su una griglia e contare il numero di celle con cui si interseca.
Inizialmente, ci sono 88 celle che si intersecano. Se scaliamo la linea di costa di un fattore 2, ci sono 197 celle intersecanti – più del doppio!
La dimensione della linea di costa è aumentata di un fattore 19788. Come prima, questo significa che la dimensione della linea costiera è
d=log219788≈1.16
Se ripetiamo questo con griglie più grandi, scopriremo che la dimensione della linea costiera della Gran Bretagna è in realtà circa 1,21. Mandelbrot si rese conto che questa dimensione frattale è anche una misura della rugosità di una forma – un nuovo concetto, per il quale trovò importanti applicazioni in molte altre aree della matematica e della scienza.
Altri frattali in natura e tecnologia
Mentre i veri frattali non possono mai apparire in natura, ci sono molti oggetti che sembrano quasi frattali. Abbiamo già visto piante, fiocchi di neve e coste, ed ecco altri esempi:
Catena montuosa nell’Asia centrale
Delta del fiume Gange in India
Fulmini
Vasi sanguigni nella retina
Grand Canyon negli USA
Nuvole
Tutti questi oggetti potrebbero sembrare completamente casuali, ma, proprio come i frattali, c’è un modello sottostante che determina come si formano. La matematica può aiutarci a capire meglio le forme, e i frattali hanno applicazioni in campi come la medicina, la biologia, la geologia e la meteorologia.
Terreno frattale generato dal computer
Possiamo anche usare i frattali per creare “copie” realistiche della natura, per esempio, come paesaggi e texture usati nei videogiochi o nei film generati dal computer. L’acqua, le montagne e le nuvole in questa immagine sono fatte interamente da un computer, con l’aiuto di frattali!
E possiamo anche invertire questo processo per comprimere le immagini digitali, per ridurre le dimensioni dei file. I primi algoritmi sono stati sviluppati da Michael Barnsley e Alan Sloan negli anni ’80, e ancora oggi se ne studiano di nuovi.