Che cos’è la frequenza? La frequenza è “quanto spesso” accade qualcosa. Poiché il suono è una vibrazione, usiamo la frequenza per descrivere quanto spesso qualcosa sta vibrando. La frequenza si misura in Hertz (Hz), che è semplicemente “quanto spesso al secondo”. Quindi, qualcosa che oscilla a 1 Hz sta vibrando una volta al secondo. Una vibrazione “completa” è chiamata “ciclo”, misurato su un picco e una depressione completi di un’onda (cioè la massima distanza o ‘ampiezza’ sopra il punto centrale o ‘0’, rappresentato sull’asse x). (Nei primi giorni della musica elettronica, i termini “cicli al secondo” erano usati al posto di Hz, che potete vedere su molti sintetizzatori vecchi/vintage oggi).
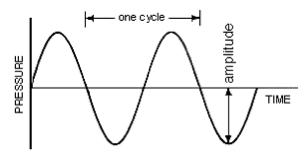
L’immagine sopra è un’onda sinusoidale – la rappresentazione più pura di una singola frequenza o vibrazione. Il tempo necessario all’onda per completare un ciclo è la frequenza dell’onda (di nuovo, “quanto spesso” sta vibrando). Più vibrazioni al secondo (cioè oscillazioni più veloci) producono frequenze sonore “più alte” e meno vibrazioni al secondo (cioè oscillazioni più lente) producono frequenze sonore “più basse”. Gli esseri umani possono sentire solo frequenze approssimativamente tra 20Hz – 20.000Hz (20kHz) (per saperne di più vedi https://en.wikipedia.org/wiki/Hearing_range).
Nella musica, i termini frequenza, altezza e tono sono correlati.Un tono è un suono con una o più frequenze identificabili. La frequenza è la misura empirica di un fenomeno fisico, definita come i cicli (di vibrazione) al secondo. L’altezza è una percezione soggettiva dell’altezza relativa di un tono, come “alto” o “basso” (per saperne di più vedi Modelli concettuali e Mappatura interdisciplinare di Lawerence Zbikowski http://zbikowski.uchicago.edu/pdfs/ZbikowskiConceptualmodels_1997.pdf).
Mentre le frequenze sono rappresentate con numeri (Hz), l’altezza è rappresentata con lettere. Per esempio, se avete mai sentito un’orchestra ‘accordare’ all’inizio di un concerto, un singolo suonatore (di solito un oboe o un violino) suona un ‘A’ misurato a 440Hz (indicato come A440). Con l’intonazione, usiamo solo le lettere A, B, C, D, E, F e G (altri simboli sono usati per alzarle o abbassarle, più avanti). Queste altezze si ripetono ogni 8 note, chiamate ottave. Per differenziare le ottave a cui ci si riferisce quando si parla di altezza, si aggiunge un numero dopo la lettera. Per esempio, A440(Hz) si chiama A4 in termini di altezza. Non confondetevi però, il 4 si riferisce all’ottava in cui ci riferiamo a quel particolare La (specificamente sul pianoforte) – è solo una coincidenza che la frequenza sia 440, il 4 non si riferisce specificamente a quello. Ma perché allora A4 è 440 Hz, vi chiederete… beh, c’è una risposta piuttosto complicata a questa domanda, ma alla fine è davvero arbitraria. In parole povere, un gruppo di persone si è riunito nel XIX secolo e ha deciso che era così. (Se volete saperne di più sull’argomento fate qualche ricerca su A440 o sugli standard di intonazione https://en.wikipedia.org/wiki/A440 (pitchstandard)).
È importante notare che la frequenza è assoluta, mentre l’intonazione è relativa (questi cambiamenti relativi sono chiamati ‘accordatura’). Usiamo le altezze per descrivere la loro relazione (cioè il rapporto) con altre altezze e l’analisi di queste relazioni è la base della ‘teoria musicale’. In generale, abbiamo concordato che A4 è definito come l’altezza la cui frequenza è 440 Hz (un riferimento assoluto). Possiamo poi determinare il ‘pitch’ o ‘tuning’ di tutte le altre note in relazione a questo usando una particolare formula di accordatura.
Un aspetto molto importante di tutta la teoria musicale è che le ottave sono specificamente definite come ‘raddoppiando’ o ‘dimezzando’ la frequenza di un pitch. Per esempio, le frequenze 220 Hz, 440 Hz e 880 Hz sono tutte A, ma esistono in ottave diverse: A3, A4 e A5 rispettivamente. Nella teoria musicale occidentale, abbiamo generalmente (e francamente, arbitrariamente) concordato che all’interno di ogni ottava ci sono 12 suddivisioni o altezze uguali. Quindi come facciamo a determinare dove queste altre note sono ‘accordate’ in relazione a quell’A440? Bene, dopo molti anni di sperimentazione è stato deciso che la seguente formula determina il rapporto relativo tra le altezze (più specificamente, la frequenza f dell’ennesimo tasto su un pianoforte standard):
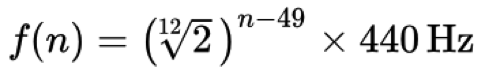https://en.wikipedia.org/wiki/Pianokeyfrequencies
In parole povere, ogni tono/punto nell’accordatura della musica classica occidentale è derivato partendo da A440 come “tono di riferimento” e poi moltiplicando o dividendo per la dodicesima radice di due (~1.059463) per ottenere un altro tono sopra o sotto quel tono di riferimento. Il numero 49 in questo caso è arbitrario (A4 è il 49° tasto sulla tastiera standard del pianoforte) e nella computer music usiamo tipicamente i numeri MIDI per i nostri calcoli – A440 è il tasto MIDI numero 69 per esempio (più sugli standard MIDI in una lezione separata).
Si deve notare che questa formula rappresenta solo un particolare stile di ‘accordatura’ che esiste all’interno della tradizione della musica classica occidentale ed è usata in generale come lo ‘standard mondiale’ quando si parla di relazioni altezza/frequenza/tonalità in generale, anche se queste relazioni sono arbitrarie e altri sistemi di accordatura esistono all’interno di diverse culture e tradizioni. Questo sistema mantiene un’importante ‘regola’ che le ottave sono definite come esatto raddoppio o inversione delle frequenze, pur mantenendo gli stessi rapporti (pitch) di dividere ogni ottava in 12 parti uguali. Chiamiamo questo sistema di accordatura 12-tone equaltemperament e serve come base per la maggior parte del mondo come sistema di accordatura fondamentale e concordato, specialmente quando si tratta della standardizzazione delle apparecchiature musicali elettroniche. (Tutti i pianoforti sono accordati in questo sistema e tutti i dati MIDI seguono questo principio generale).
Nella terminologia musicale, descriviamo le altezze (o toni) come ascendenti o discendenti in termini di ‘passi’. Ci sono due tipi di passi: mezzi passi e passi interi (chiamati anche semitoni o toni interi). Alzare le note di un mezzo passo (cioè un semitono) è indicato con un simbolo ♯ chiamato ‘diesis’ (simbolo numerico o hashtag) e abbassare i toni di un mezzo passo è indicato con un simbolo ♭ chiamato ‘bemolle’ (si usa spesso anche una ‘b’ minuscola). Puoi pensare ai semitoni o ai mezzi passi come alla distanza minima tra due tasti adiacenti del pianoforte o dei tasti della chitarra.
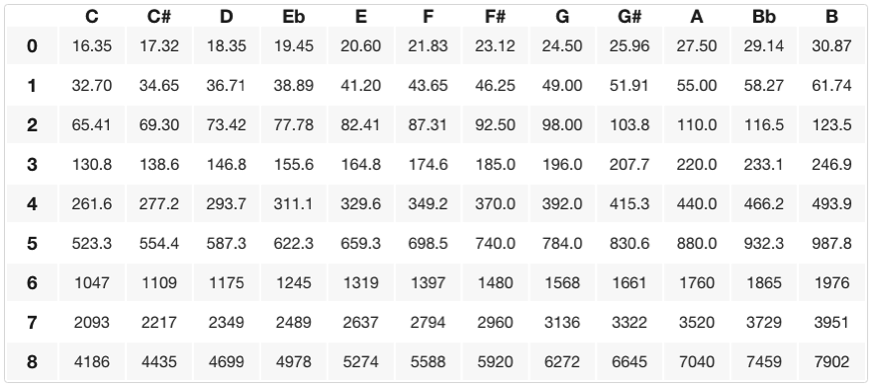
Per ottenere la frequenza di un semitono in più rispetto all’A4 moltiplichiamo 440 Hz per la dodicesima radice di due per darci ~466,2 Hz, dandoci un A# (o Bb). A# e Bb sono chiamate ‘note enarmoniche’, o altezze che sono tecnicamente la stessa frequenza ma che potrebbero essere ‘scritte’ diversamente a seconda della ‘chiave’ o del contesto musicale di cui stiamo parlando (di più su questo in una lezione separata). Per ottenere la frequenza di un intero gradino sopra l’A4 possiamo moltiplicare 440Hz due volte per la dodicesima radice di due dandoci ~493.9 Hz o B4. Sotto c’è una tabella di tutte le frequenze specifiche con la loro relazione altezza/ottava (i nomi delle note sono sull’asse delle x e i numeri delle ottave sono sull’asse delle y).
https://www.seventhstring.com/resources/notefrequencies.html
Questa collezione di ‘dodici note per ottava’ è chiamata scala cromatica.Una ‘scala’ è una collezione di note in ordine ascendente/discendente che inizia/finisce su una frequenza o altezza fondamentale. Una scala cromatica inizia su una qualsiasi altezza e sale (o scende) di 11 mezzi passi (semitoni) successivamente adiacenti dalla sua fondamentale. Sul grafico qui sopra, puoi trovare le frequenze specifiche o le note/punte di qualsiasi scala cromatica iniziando su una data nota (la fondamentale) e contando su o giù per 11 semitoni (altezze adiacenti).
Se hai notato, alcune delle note nel grafico qui sopra sono ‘scritte’ con un # (diesis) mentre altre sono scritte con un b (bemolle). Teoricamente, qualsiasi nota può essere alzata o abbassata di un mezzo o intero passo/tonalità aggiungendo uno di questi simboli dopo di essa. Tuttavia, ci sono convenzioni che certe note sono ‘scritte’ in un modo particolare data la prevalenza e la prevedibilità delle pratiche della teoria musicale occidentale. Per quanto riguarda le ‘grafie enarmoniche’ delle note e delle altezze (note che hanno la stessa frequenza ma sono rappresentate come altezze diverse), la tabella qui sopra rappresenta le grafie più comuni delle note e delle altezze in relazione alle pratiche tradizionali delle ‘firme di chiave’ in musica, ma non include tutte le possibilità. Le seguenti note sono comuni grafie enarmoniche (le barre indicano che le note/punte sono della stessa frequenza ma possono essere rappresentate o ‘scritte’ come altezze diverse):
C#/Db D#/Eb F#/Gb G#/Ab A#/Bb
Ovviamente, teoricamente ogni nota può essere alzata o abbassata di un mezzo passo (semitono) o anche di un intero passo (tono intero) con un simbolo # o b e la teoria musicale più avanzata entra in quelli che sono chiamati doppi bemolle e diesis.Senza diventare troppo complicati o profondi, tutte le scale o chiavi musicali sono una collezione di mezzi passi e passi interi e l’ortografia di quei passi dà all’esecutore indizi sulle relazioni (cioè rapporti) tra le altezze che il compositore sta usando.
- Hertz (Hz)
- frequenza
- tono
- punto
- A4 (A440)
- ottavi
- passi interi (toni interi)
- mezzi passi (semitoni)
Sé-Quiz
- Il passo G3 ha una frequenza fondamentale di 196Hz. Senza consultare una tabella, quali sono le frequenze delle altezze G2 e G4 (un’ottava sotto e sopra G4)?
Risorse aggiuntive
- Proprietà del suono – Khan Academy
- Suono: Crash Course Fisica