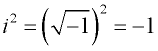Valore negativo sotto la radice quadrata radicale – MathBitsNotebook (A1

Indaghiamo su cosa succede quando valori negativi appaiono sotto il simbolo radicale (come radicando) per radici cubiche e radici quadrate.

In alcune situazioni, i numeri negativi sotto un simbolo radicale sono OK. Per esempio, non è un problema poiché (-2) – (-2) – (-2) = -8, rendendo la risposta -2. Nei problemi di radici cubiche, è possibile moltiplicare un valore negativo per se stesso tre volte e ottenere una risposta negativa.

Le difficoltà, tuttavia, si sviluppano quando guardiamo un problema come . Questo problema di radice quadrata chiede un numero moltiplicato per se stesso che darà un prodotto (risposta) di -16. Semplicemente non c’è modo di moltiplicare un numero per se stesso e ottenere un risultato negativo. Considera che: (4) – (4) = 16 e (-4) – (-4) = 16.

RADICI DEL CUBO:	Ma	RADICI QUADRATE:
Sì, (-2) x (-2) x (-2) = -8. Nessun problema.		No! (4) x (4) ≠ -16. No! (-4) x (-4) ≠ -16.

Le radici quadrate sono i colpevoli! Le difficoltà sorgono quando si incontra un valore negativo sotto una radice quadrata. Non è possibile elevare al quadrato un valore (moltiplicarlo per se stesso) e arrivare a un valore negativo. Quindi, cosa facciamo?

La radice quadrata di un numero negativo non esiste nell’insieme dei numeri reali. Vedevano equazioni come x2 + 1 = 0, e si chiedevano cosa significasse davvero la soluzione . Nel tentativo di affrontare questo problema, i matematici “crearono” un nuovo numero, i, che fu chiamato “numero immaginario”, poiché non era nell’insieme dei “numeri reali”. Questo nuovo numero fu visto con molto scetticismo. Il numero immaginario apparve per la prima volta in stampa nell’anno 1545. Il numero immaginario “i” è la radice quadrata di uno negativo. Un numero immaginario possiede la proprietà unica che quando viene elevato al quadrato, il risultato è negativo. 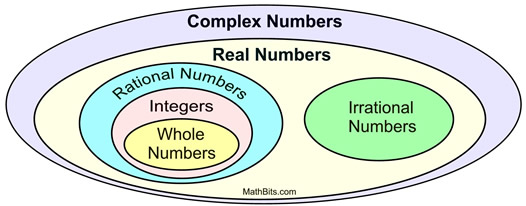Considera: Il processo di semplificazione di un radicale contenente un fattore negativo è lo stesso della normale semplificazione dei radicali. L’unica differenza è che il sarà sostituito da una “i “. Con il proseguire della ricerca sui numeri immaginari, si scoprì che essi in realtà colmavano una lacuna nella matematica e servivano ad uno scopo utile. I numeri immaginari sono essenziali per lo studio di scienze come l’elettricità, la meccanica quantistica, l’analisi delle vibrazioni e la cartografia. Quando la i immaginaria fu combinata con l’insieme dei numeri reali, si formò l’insieme onnicomprensivo dei numeri complessi.