オイラーの恒等式は、シェイクスピアのソネットに例えられ、「最も美しい方程式」と評される数学で見られる等式です。 これは、偉大な物理学者である故リチャード・ファインマンが講義の中で “我々の宝石”、”数学で最も驚くべき式” と呼んだオイラーの式という複素数演算の基礎方程式の特殊なケースである。
数学とその応用研究所のデビッド・パーシー教授は、BBCのインタビューで、オイラーの恒等式は「本当の古典で、これ以上のものはない…見るからにシンプルだが、信じられないほど深遠で、最も重要な5つの数学定数から構成されている」と語っています。”
オイラーの恒等式は簡単に書くと:eiπ + 1 = 0
5つの定数は:
- 数 0.
- 数 1.
- 数 π、円の周とその直径との比であり非理数(桁数が終わらない)のことである。 およそ3.14159…
- 数e、これも無理数である。 複利や微積分を学ぶことで自然に発生する自然対数の底となる数である。 eという数は数学に広く浸透しており、膨大な数の重要な方程式にどこからともなく現れるようなものである。 約2.71828…<7881><8679>数iは、負の1の平方根として定義される。 √(-1). 虚数の中で最も基本的な数で、現実にはどの数もそれ自体を掛けて負の数になることはない(したがって、負の数には実際の平方根はない)ので、このように呼ばれています。 しかし、数学の世界では、やむを得ず負の平方根を取らなければならない場面が多々ある。 7881>
Prolific mathematician
Leonhard Eulerは18世紀のスイス生まれの数学者で、現代の数学に不可欠な多くの概念を開発した。 彼はキャリアのほとんどをロシアのサンクトペテルブルクで過ごした。 米国海軍兵学校(USNA)によると、彼は史上最も多作な数学者の一人であり、886の論文と書籍が出版されました。 彼の業績の多くは、全盲であった晩年の20年間にもたらされたものである。
オイラーの重要な貢献には、オイラーの公式とオイラーの定理があり、どちらも文脈によって異なる意味を持ちます。 USNAによると、力学では「オイラー角(剛体の向きを指定する)、オイラーの定理(すべての回転には軸がある)、流体の運動に関するオイラー方程式、オイラー・ラグレンジ方程式(変分法に由来する)」があるそうです。「
複素数の掛け算
オイラー恒等式は、実数と虚数の2つからなる数である複素数の相互作用から自然に生まれたもので、例としては4+3iがある。 複素数は、量子力学の中の波動力学や、電気工学の中の交流電流を使う回路の設計など、さまざまな用途で登場します。 さらに、複素数には、コンピュータグラフィックス、ロボット工学、ナビゲーション、飛行力学、軌道力学の研究に特に役立つ性質がある。 この性質は、オイラーの恒等式の背後にある理由を理解するのに役立ちます。
以下の例では、5 つの複素数が複素平面上にプロットされ、一緒に「家の形」を形成しています。 複素数平面とは、2次元であることを除けば、数直線に似ています。 横方向が実数、縦軸が虚数を表しています。 それぞれの家型の複素数に複素数4+3iを掛けて再プロットしています(緑色の矢印)。
見てわかるように、4+3iを掛けると、家の形は拡張(面積が大きくなり、原点0+0iから同じだけ離れる)し、回転(ある角度だけ傾く)することがわかります。 これがまさに4+3iの掛け算の効果であることを示すために、家を5倍に拡大して36.9度回転させた場合の効果も示しています(赤矢印)。
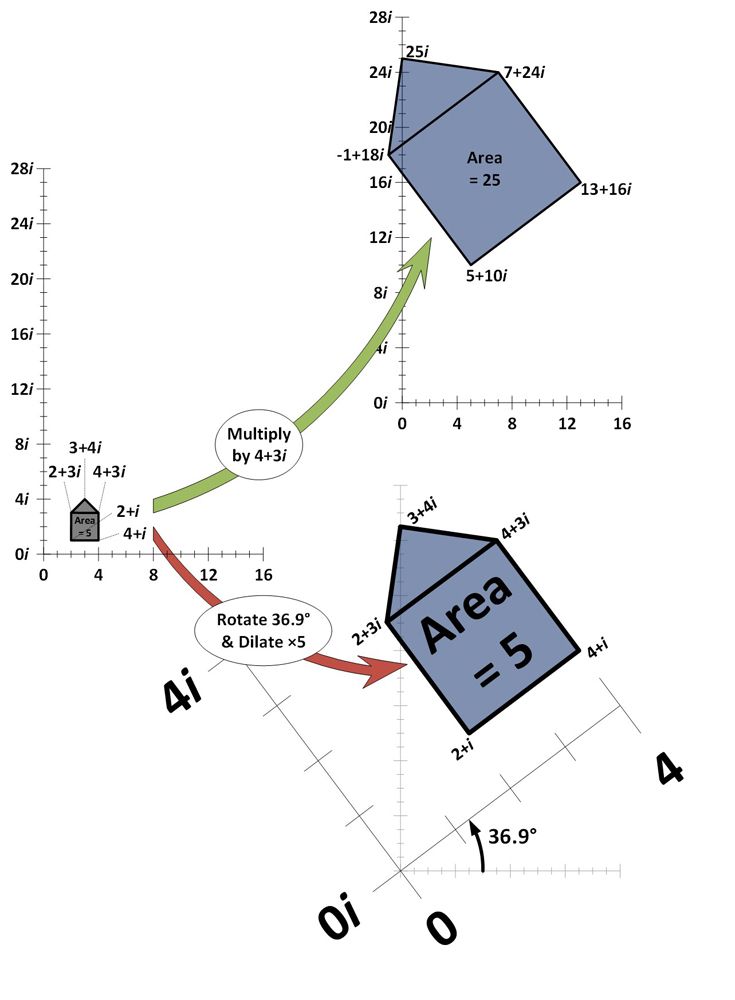
異なる量の拡張と回転により、複素平面上の任意の数の乗算の効果を生み出すことができる。
複素数の極形式
回転と拡張の量は、下の図に見られるように、原点から5単位(r = 5)、水平軸と36.9度の角(φ = 36.9°)を成す数4+3iの固有の性質によって決定される。 5969>
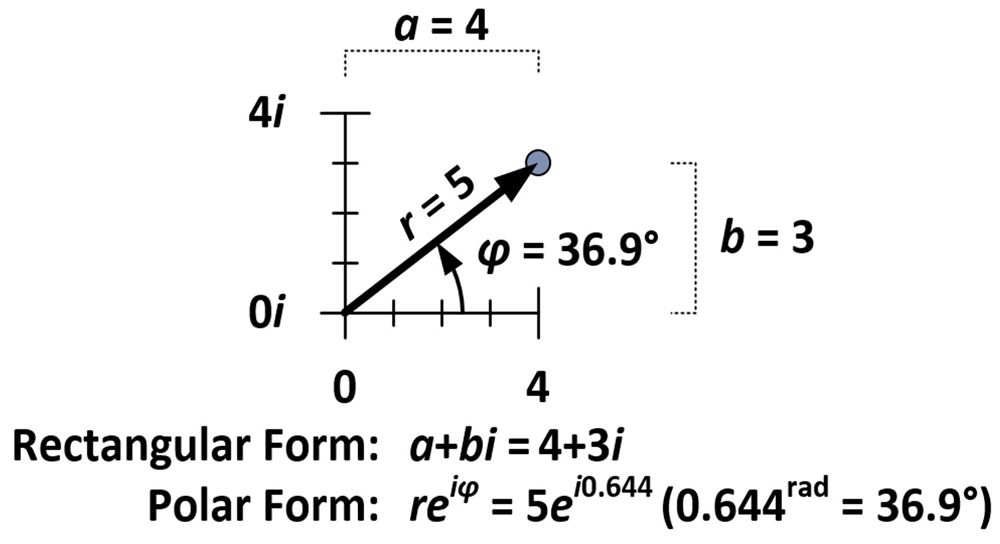
極形式では、φをラジアン単位で測定する必要があります。 1ラジアン(1rad)は約57.3度で、円の半径を円周に巻き付けた時の角度の尺度である。 πラジアンは円の半周を、2πラジアンは1周を包む。
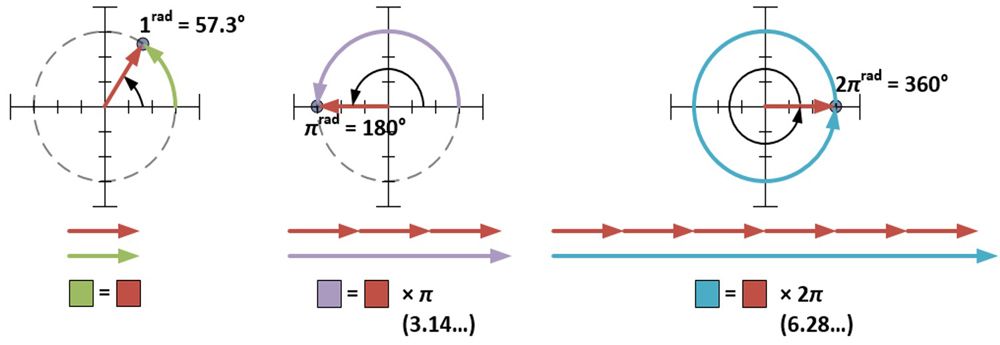
4+3i の角度の測度は 0.644 ラジアン (36.9° = 0.644rad) で、4+3i の極形式は 5ei0.644 になる。 また、各家形点のrとφの測度も求められるが、4+3iの掛け算による拡張/回転効果を得るには、各rを5倍し、各φに36.9度(0.644ラド)を加える方法もある。 このデモから、複素数同士を掛け合わせると、距離は乗算され、角度は加算されることがわかる。
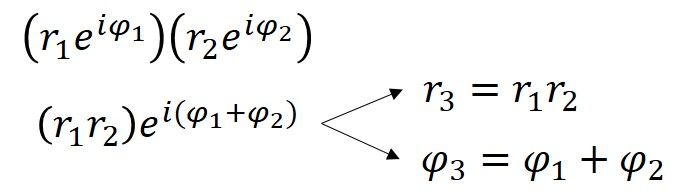
複素数の極形式が確立されると、オイラーの恒等式の問題は、a=-1、b=0 の a+bi の特殊例に過ぎない。 その結果、極形式reiφについては、r=1、φ=πとなります(πrad=180°なので)。
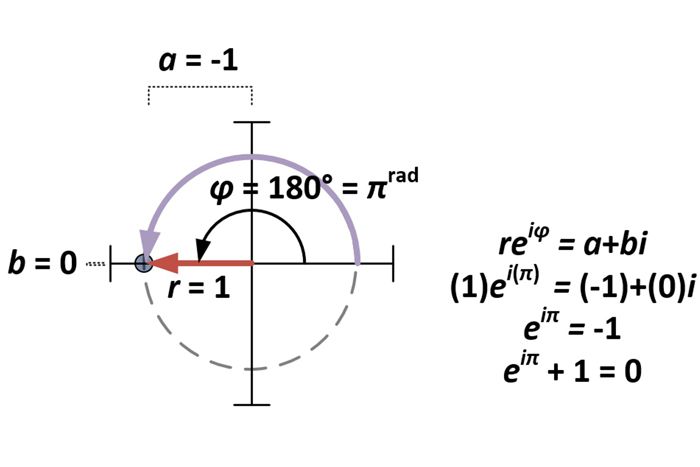
極形式の導出
Euler の恒等式は複素数の極形式から導かれるが、微積分なしでは極形式(特に数 e の自発的出現)は導出できない
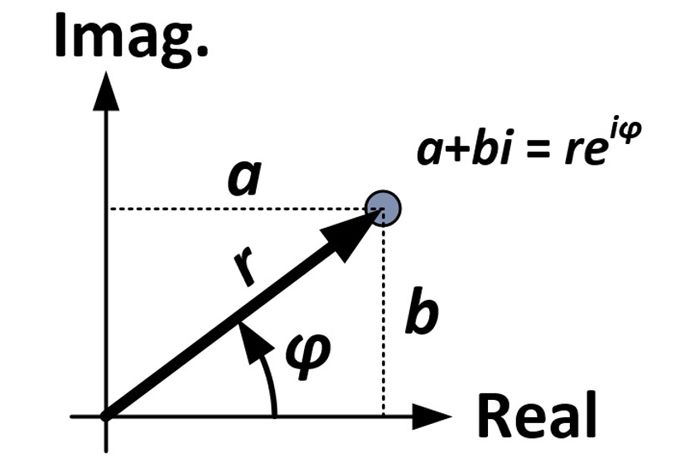
複素数の矩形形から始めます:
a + bi
図と三角法から、次のように代入できます。
(r-cosφ) + (r-sinφ)i
ここからrを因数分解すると:
r-(cosφ + i-sinφ)
“cosφ + i-sinφ” を cisφ と呼ぶこともあり、これは「余弦+虚正弦」の略語である。”
r-cisφ
関数cisφはeiφと等しいことがわかります。 これは微積分をしないと示せない部分です。

したがって、方程式 r-cisφ は標準極形式 r-eiφ.
で記述される。