Wanneer je in de natuur rondkijkt, zijn je misschien ingewikkelde planten als deze opgevallen:


Deze varen bestaat uit vele kleine blaadjes die zich vertakken van een groter blad.


Deze Romanesco broccoli bestaat uit kleinere kegelvormige bolletjes die zich spiraalsgewijs rond een groter bolletje bevinden.
Op het eerste gezicht lijken dit uiterst complexe vormen – maar als u beter kijkt, ziet u dat ze allebei een betrekkelijk eenvoudig patroon volgen: alle afzonderlijke delen van de plant zien er precies hetzelfde uit als de hele plant, alleen kleiner. Hetzelfde patroon herhaalt zich steeds weer, op kleinere schaal.
In de wiskunde noemen we deze eigenschap zelfgelijkvormigheid, en vormen die dit hebben worden fractals genoemd. Ze behoren tot de mooiste en meest bizarre objecten in de wiskunde.
Om onze eigen fractals te maken, moeten we beginnen met een eenvoudig patroon en dat steeds herhalen, op kleinere schaal.
Een van de eenvoudigste patronen kan een lijnstuk zijn, met aan één uiteinde nog twee lijnstukken die zich vertakken. Als we dit patroon herhalen, zullen beide blauwe segmenten ook twee vertakkingen aan hun uiteinden hebben.
Je kunt de blauwe stippen verplaatsen om de lengte en de hoek van alle vertakkingen te veranderen. Verhoog vervolgens het aantal iteraties met de schuifknop eronder.
Afhankelijk van de positie van de takken, kun je totaal verschillende patronen maken – lijkend op de varen hierboven, een boom, of geneste vijfhoeken. Wat kun je nog meer vinden?
Een andere bekende fractal is de Sierpinski driehoek. In dit geval beginnen we met een grote, gelijkzijdige driehoek, en knippen dan herhaaldelijk kleinere driehoeken uit de overblijvende delen.
Merk op hoe de uiteindelijke vorm bestaat uit drie identieke kopieën van zichzelf, en elk van deze kopieën bestaat uit nog kleinere kopieën van de hele driehoek! Je zou eindeloos op de driehoek kunnen blijven inzoomen, en de patronen en vormen zullen zich altijd blijven herhalen.
De planten aan het begin van dit hoofdstuk zien er uit als fractals, maar het is duidelijk onmogelijk om in het echt echte leven echte fractals te maken. Als we hetzelfde patroon steeds maar weer zouden herhalen, kleiner en kleiner, dan zouden we uiteindelijk tot cellen, moleculen of atomen komen die niet meer te splitsen zijn.
Met behulp van wiskunde kunnen we echter wel nadenken over de eigenschappen die echte fractals “zouden” hebben – en die zijn heel verrassend…
Fractale dimensies
Laten we eerst eens nadenken over de dimensie van fractals. Een lijn heeft dimensie . Bij schaling met een factor 2 neemt de lengte toe met een factor 21=2. Dat is duidelijk! Een vierkant heeft dimensie . Bij schaling met een factor 2 neemt de oppervlakte toe met een factor 22= .
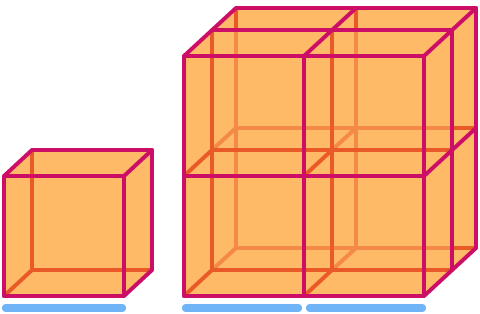
Een kubus heeft afmeting . Als we hem schalen met een factor 2, neemt zijn volume toe met een factor 23= . Merk op dat de grotere kubus in de afbeelding bestaat uit 8 kopieën van de kleinere!
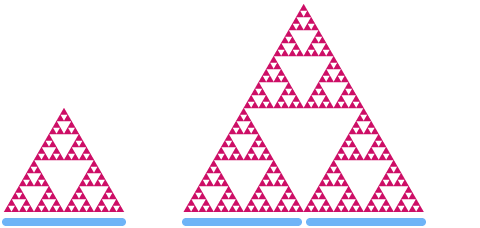
Nu gaan we eens kijken naar de Sierpinski driehoek. Als we hem schalen met een factor 2, dan zie je dat zijn “oppervlakte” toeneemt met een factor .
Laten we zeggen dat d de afmeting is van de Sierpinski driehoek. Gebruikmakend van hetzelfde patroon als hierboven, krijgen we 2d=3. Met andere woorden, d = log23log32 ≈ 1.585…
Maar wacht … hoe kan iets een dimensie hebben die geen geheel getal is? Het lijkt onmogelijk, maar dit is juist een van de vreemde eigenschappen van fractals. Hieraan ontlenen fractals hun naam: ze hebben een fractionele dimensie.
Met elke iteratie nemen we een deel van de oppervlakte van de Sierpinski-driehoek weg. Als we dit oneindig vaak zouden kunnen doen, zou er eigenlijk geen oppervlakte meer over zijn: daarom houdt de Sierpinski-driehoek het midden tussen een tweedimensionaal gebied, en een eendimensionale lijn.
Weliswaar zijn veel fractals self-similar, maar een betere definitie is dat fractals vormen zijn die een niet-integer dimensie hebben.
De Koch-sneeuwvlok
Er zijn veel vormen in de natuur die op fractals lijken. We hebben aan het begin van dit hoofdstuk al wat planten gezien. Andere mooie voorbeelden zijn sneeuwvlokken en ijskristallen:
Om onze eigen fractale sneeuwvlok te maken, moeten we opnieuw een eenvoudige procedure vinden die we steeds opnieuw kunnen toepassen.
Zoals de Sierpinski driehoek, beginnen we met een enkele, gelijkzijdige driehoek. Maar in plaats van bij elke stap kleinere driehoeken te verwijderen, voegen we langs de rand kleinere driehoeken toe. De zij-lengte van elke driehoek is 131412 van de driehoeken in de vorige stap.
De resulterende vorm heet de Koch sneeuwvlok, genoemd naar de Zweedse wiskundige Helge von Koch. Merk opnieuw op dat kleine delen van de rand van de sneeuwvlok er precies hetzelfde uitzien als grotere delen.
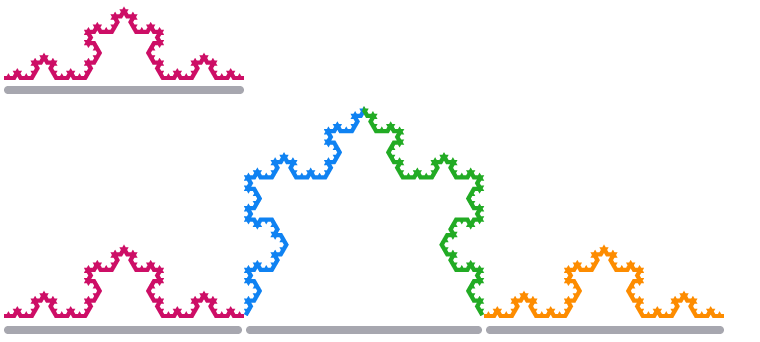
Wanneer we één randsegment van de Koch sneeuwvlok met een factor 3 schalen, verviervoudigen we de lengte ervan.
Gebruik makend van dezelfde relatie tussen afmetingen en schaalfactoren als hierboven, krijgen we de vergelijking 3d=42d=42d=34d=3. Dit betekent dat de afmeting van de Koch sneeuwvlok d=log34≈1.262 is.
Area
Het maken van de Koch sneeuwvlokken is bijna als een recursieve reeks: we kennen de beginvorm (een driehoek), en we weten hoe we van de ene term naar de volgende moeten komen (door aan elke rand meer driehoeken toe te voegen):


nieuwe driehoeken

nieuwe driehoeken

nieuwe driehoeken
Na de eerste iteratie neemt het aantal toegevoegde nieuwe driehoeken bij elke stap toe met een factor van. Tegelijkertijd neemt de oppervlakte van deze nieuwe driehoeken bij elke stap met een factor af.
Stel dat de eerste driehoek een oppervlakte heeft van 1. Dan is de totale oppervlakte van de volgende drie drie driehoeken 3×19=13. De volgende stappen vormen allemaal een meetkundige reeksaritmetische reeksquadratische reeks, met gemeenschappelijke verhouding 499443.
Met behulp van de formule voor de som van oneindige meetkundige reeksen kunnen we uitrekenen dat de totale oppervlakte van de Koch sneeuwvlok
A=1+13×11-491+949-14=85=1 is.6.
Omtrek
We kunnen ook proberen om de omtrek van de Koch sneeuwvlok te berekenen. Zoals we al eerder hebben gezien, verandert de lengte van de omtrek bij elke stap met een factor 433414.
Dit betekent dat we weer een meetkundige reeks hebben – maar in dit geval convergeert hij niet naar 0heeft hij geen eerste term. Dit betekent dat de omtrek van de Koch sneeuwvlok in feite oneindig lang is!

Als dit contra-intuïtief lijkt, bedenk dan dat we de omtrek bij elke stap met 43 vermenigvuldigen, en dat we dit oneindig vaak doen.
Het is bijna ondenkbaar dat je een vorm kunt hebben met een eindige oppervlakte en tevens een oneindige omtrek – maar dit is slechts een van de vele onverwachte eigenschappen van fractals.
Kun je nog andere manieren bedenken om je eigen fractals te maken?
“Mijn ziel spiraliseert op bevroren fractals rondom…”
Menger Sponge
Fractals hoeven niet “plat” te zijn, zoals veel van de voorbeelden hierboven. Een van de beroemdste fractals die er driedimensionaal uitzien is de Menger-spons, genoemd naar de wiskundige Karl Menger die hem in 1926 voor het eerst beschreef.
We beginnen met een massieve kubus, en boren herhaaldelijk steeds kleinere gaatjes in de zijden. Elke nieuwe iteratie van gaten heeft 131214 de breedte van de vorige iteratie van gaten.
Een kubus van 3×3×3 bestaat uit 27 kleinere kubussen, maar hier hebben we er een aantal verwijderd. De Menger-spons bestaat uit kopieën van zichzelf, die 3 keer zo klein zijn.
Nu kunnen we proberen de dimensie d van de Menger-spons te berekenen, net zoals we dat hierboven voor de Koch-sneeuwvlok hebben gedaan. In dit geval krijgen we 3d=20, of d=log320≈2.727.
Als je je voorstelt dat je steeds meer gaten uitsnijdt, oneindig veel keer, dan zou er geen werkelijk volume meer over zijn. Daarom is de kubus “niet helemaal” driedimensionaal!
Fractale kustlijnen
Eén van de belangrijkste kenmerken van alle fractals die we tot nu toe hebben gezien, is dat je eindeloos kunt “inzoomen” en steeds nieuwe patronen vindt. Rond 1920 realiseerde de Britse wiskundige Lewis Fry Richardson zich dat dit ook geldt voor de grens of kustlijn van veel landen.
Je begint met de basisvorm van het land, en als je inzoomt, voeg je rivierinhammen, baaien en estuaria toe, dan individuele kliffen, rotsen, kiezelstenen, enzovoort:
Dit is een belangrijk probleem wanneer je de lengte van de grens van een land probeert te berekenen – hoe beslis je hoe ver je moet inzoomen, en welke hoekjes en gaatjes je moet opnemen?
Een manier om de lengte van de Britse kustlijn te meten is bijvoorbeeld een lange liniaal te nemen, helemaal langs de stranden te lopen, en dan alle afstanden op te tellen.
Als de liniaal ${rulers}km lang is, moeten we hem ${count} keer gebruiken, dus krijgen we een totale kustlijn van ${count} × ${rulers} = ${count * rulers}km.
We kunnen gewoon doorgaan, met steeds kleinere linialen, en elke keer zou ons resultaat voor de lengte van de kustlijn een beetje langer worden. Net als de Koch Snowflake hiervoor, lijkt het erop dat de kustlijn van Groot-Brittannië oneindig lang is! Dit wordt vaak de kustlijnparadox genoemd.
Een paar decennia later stuitte de wiskundige Benoit Mandelbrot op het werk van Richardson in een afgedankt bibliotheekboek, toen hij bij IBM werkte. Hij zag het belang ervan in, en ook hoe het verband hield met recenter onderzoek naar fractals en dimensies.
De kustlijn van Groot-Brittannië “ziet er” zeker fractal uit, maar hij is niet zelfgelijkvormig, zoals andere fractals die we eerder hebben gezien. Om de grootte te bepalen, kunnen we de kustlijn op een raster tekenen en het aantal cellen tellen waarmee zij wordt doorsneden.
In het begin zijn er 88 cellen die elkaar snijden. Als we de kustlijn met een factor 2 schalen, zijn er 197 doorsnijdende cellen – meer dan twee keer zo veel!
De grootte van de kustlijn is toegenomen met een factor 19788. Net als voorheen betekent dit dat de dimensie van de kustlijn
d=log219788≈1.16
Als we dit herhalen met grotere rasters, vinden we dat de dimensie van de kustlijn van Groot-Brittannië in feite ongeveer 1.21 is. Mandelbrot realiseerde zich dat deze fractale dimensie ook een maat is voor de ruwheid van een vorm – een nieuw concept, waarvoor hij belangrijke toepassingen vond in vele andere gebieden van de wiskunde en de wetenschap.
Meer fractals in de natuur en de technologie
Terwijl echte fractals nooit in de natuur kunnen voorkomen, zijn er veel voorwerpen die er bijna als fractals uitzien. We hebben al planten, sneeuwvlokken en kustlijnen gezien, en hier zijn nog een paar voorbeelden:
Bergketen in Centraal-Azië
Ganges rivierdelta in India
Bliksemschichten
Bloedvaten in het netvlies
Grand Canyon in de VS
Wolken
Al deze objecten lijken misschien volkomen willekeurig, maar net als bij fractals is er een onderliggend patroon dat bepaalt hoe ze gevormd worden. Wiskunde kan ons helpen de vormen beter te begrijpen, en fractals hebben toepassingen op gebieden als geneeskunde, biologie, geologie en meteorologie.
Computergegenereerd fractaal terrein
We kunnen fractals ook gebruiken om realistische “kopieën” van de natuur te maken, bijvoorbeeld als landschappen en texturen die worden gebruikt in videospelletjes of computergegenereerde films. Het water, de bergen en de wolken in dit beeld zijn volledig door de computer gemaakt, met behulp van fractals!
En we kunnen dit proces zelfs omkeren om digitale beelden te comprimeren, om hun bestandsgrootte te verkleinen. De eerste algoritmen zijn in de jaren tachtig ontwikkeld door Michael Barnsley en Alan Sloan, en er wordt nog steeds onderzoek gedaan naar nieuwe algoritmen.