Frequentie en toonhoogte

Wat is frequentie? Frequentie is “hoe vaak” iets gebeurt. Aangezien geluid trillingen zijn, gebruiken we frequentie om aan te geven hoe vaak iets trilt. Frequentie wordt gemeten in Hertz (Hz), gewoon “hoe vaak per seconde”. Iets dat met 1 Hz trilt, trilt dus één keer per seconde. Een “volledige” trilling wordt een “cyclus” genoemd, gemeten aan één volledige piek en dal van een golf (d.w.z. de maximale afstand of “amplitude” boven het midden- of “0”-punt, weergegeven op de x-as). (In de begindagen van de elektronische muziek werd de term “cycli per seconde” gebruikt in plaats van Hz, die u tegenwoordig op veel oude synthesizers aantreft).

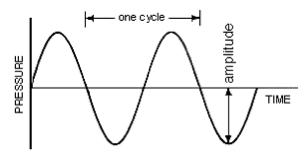
Het bovenstaande plaatje is een sinusgolf – de zuiverste weergave van een enkele frequentie of trilling. De tijd die de golf nodig heeft om één cyclus te voltooien is de frequentie van de golf (nogmaals, “hoe vaak” hij trilt). Meer trillingen per seconde (d.w.z. snellere oscillaties) produceren “hogere” geluidsfrequenties en minder trillingen per seconde (d.w.z. langzamere oscillaties) produceren “lagere” geluidsfrequenties. De mens kan alleen frequenties horen die ruwweg liggen tussen 20Hz – 20.000Hz (20kHz) (voor meer zie https://en.wikipedia.org/wiki/Hearing_range).

In de muziek zijn de termen frequentie, toonhoogte en toon verwant.Een toon is een geluid met één of meer identificeerbare frequenties. Frequentie is de empirische meting van een natuurkundig verschijnsel, gedefinieerd als het aantal trillingscycli per seconde. Toonhoogte is een subjectieve perceptie van de relatieve hoogte van een toon, zoals in ‘hoog’ of ‘laag’ (voor meer hierover zie Conceptual Modelsand Cross-Domain Mapping door Lawerence Zbikowskihttp://zbikowski.uchicago.edu/pdfs/ZbikowskiConceptualmodels_1997.pdf).

Terwijl frequenties worden weergegeven met getallen (Hz), wordt toonhoogte weergegeven met letters. Als u bijvoorbeeld ooit een orkest hebt horen ‘stemmen’ aan het begin van een concert, speelt een enkele speler (meestal een hobo of viool) een ‘A’ gemeten op 440Hz (aangeduid als A440). Voor de toonhoogte gebruiken we alleen de letters A, B, C, D, E, F, en G (extra symbolen worden gebruikt om ze te verhogen of te verlagen, waarover later meer). Deze toonhoogten herhalen zich om de 8 noten, een octaaf genoemd. Om te kunnen onderscheiden naar welke octaven we verwijzen als we het over toonhoogte hebben, wordt na de letter een cijfer toegevoegd. Bijvoorbeeld, A440 (Hz) wordt A4 genoemd in termen van toonhoogte. Maar laat u niet in verwarring brengen, de 4 verwijst naar het octaaf waarin we naar die bepaalde A verwijzen (specifiek op de piano) — het is gewoon toeval dat de frequentie toevallig 440 is, de 4 verwijst daar niet specifiek naar. Maar waarom is A4 dan 440 Hz zult u zich misschien afvragen…wel er is een nogal ingewikkeld antwoord op die vraag, maar uiteindelijk is het inderdaad willekeurig. Simpel gezegd, een stel mensen is in de 19e eeuw bij elkaar gekomen en heeft besloten dat dat het geval was. (Als u meer over het onderwerp wilt weten, doe dan wat onderzoek op A440 of pitch/tuning standardshttps://en.wikipedia.org/wiki/A440(pitchstandard)).

Het is belangrijk op te merken dat frequentie absoluut is, terwijl toonhoogte relatief is (deze relatieve veranderingen worden “tuning” genoemd). We gebruiken toonhoogten om hun relatie (d.w.z. verhouding) met andere toonhoogten te beschrijven en het analyseren van die relaties is de basis van de “muziektheorie”. In het algemeen is men het erover eens dat A4 wordt gedefinieerd als de toonhoogte waarvan de frequentie 440 Hz bedraagt (een absolute referentie). We kunnen dan de ’toonhoogte’ of ‘stemming’ van alle andere noten bepalen in relatie tot die toonhoogte met behulp van een bepaalde stemmingsformule.

Een zeer belangrijk aspect van alle muziektheorie is dat octaven specifiek worden gedefinieerd als het ‘verdubbelen’ of ‘halveren’ van de frequentie van een toonhoogte. Bijvoorbeeld, de frequenties 220 Hz, 440 Hz, en 880 Hz zijn allemaal A’s, maar bestaan in verschillende octaven: respectievelijk A3, A4 en A5. In de westerse muziektheorie zijn we het er algemeen (en eerlijk gezegd arbitrair) over eens dat er binnen elk octaaf 12 gelijke onderverdelingen of toonhoogten zijn. Dus hoe bepalen we waar deze andere noten zijn ‘gestemd’ in relatie tot die A440? Welnu, na vele jaren experimenteren is besloten dat de volgende formule de relatieve verhouding tussen de toonhoogten bepaalt (meer specifiek, de frequentie f van de n-de toets op een standaard piano):

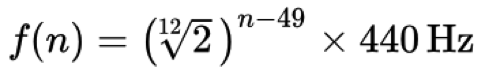https://en.wikipedia.org/wiki/Pianokeyfrequencies

Eenvoudig gezegd: elke toon/pitch in de Westerse klassieke muziekstemming wordt afgeleid door te beginnen met A440 als ‘referentietoon’ en dan te vermenigvuldigen of te delen met de twaalfde wortel uit twee (~1,059463) om tot een andere toon boven of onder die referentietoon te komen. Het getal 49 in dit geval is willekeurig (A4 is de 49ste toets op een standaard pianoklavier) en in computermuziek gebruiken we gewoonlijk MIDI-nummers voor onze berekeningen–A440 is bijvoorbeeld MIDI-sleutelnummer 69 (meer over MIDI-standaarden in een aparte les).

Het moet worden opgemerkt dat deze formule slechts één bepaalde stijl van ‘stemmen’ vertegenwoordigt die bestaat binnen de Westerse klassieke muziektraditie en in het algemeen wordt gebruikt als de ‘wereldstandaard’ als we het hebben over toonhoogte/frequentie/toon-verhoudingen in het algemeen, ook al zijn deze verhoudingen arbitrair en bestaan er andere stemsystemen binnen verschillende culturen en tradities.Dit systeem behoudt een belangrijke ‘regel’ dat octaven worden gedefinieerd als exacte verdubbeling of halvering van frequenties met behoud van dezelfde (toonhoogte) verhoudingen van het verdelen van elk octaaf in 12 gelijke delen. We noemen dit stemmingssysteem 12-toons gelijkzwevend en het dient als basis voor het grootste deel van de wereld als een fundamenteel en overeengekomen stemmingssysteem, vooral als het gaat om de standaardisatie van elektronische muziekapparatuur. (Alle piano’s zijn in dit systeem gestemd en alle MIDI-gegevens volgen dit algemene principe).

In de muziekterminologie beschrijven we toonhoogten (of tonen) als stijgend of dalend in termen van ‘stappen’. Er zijn twee soorten stappen:halve stappen en hele stappen (ook wel halve of hele tonen genoemd).Het verhogen van tonen met een halve stap (d.w.z. halve toon) wordt aangeduid met een ♯symbool dat ‘scherp’ wordt genoemd (cijfer- of hashtag-symbool) en het verlagen van tonen met een halve stap wordt aangeduid met een ♭ symbool dat ‘plat’ wordt genoemd (een kleine letter’b’ wordt ook vaak gebruikt). Je kunt halve tonen of halve stappen zien als de minimale afstand tussen twee aangrenzende pianotoetsen of gitaarfretten.

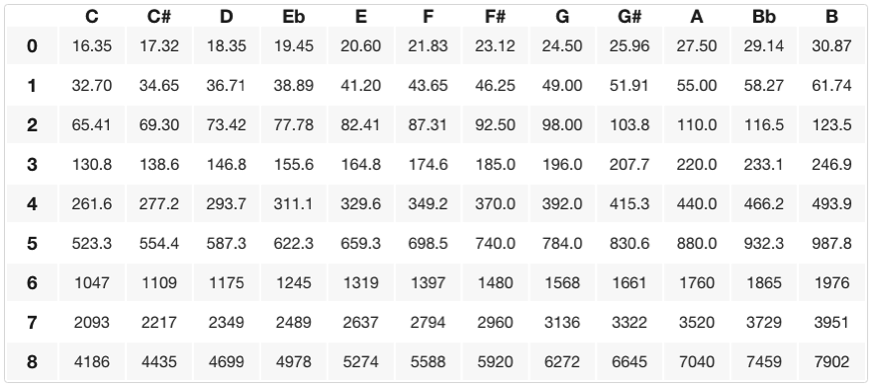
Om de frequentie een halve toon hoger te krijgen dan A4 vermenigvuldigen we 440 Hz met de twaalfde wortel van twee om ~466,2 Hz te krijgen, wat een A# (of Bb) oplevert. A# en Bb worden “enharmonische tonen” genoemd, of toonhoogten die technisch dezelfde frequentie hebben, maar anders “gespeld” kunnen worden, afhankelijk van de “toonsoort” of muzikale context waarover we het specifiek hebben (meer hierover in een afzonderlijke les). Om de frequentie een hele stap hoger te krijgen dan A4 kunnen we 440Hz tweemaal vermenigvuldigen met de twaalfde wortel uit twee wat ons ~493.9 Hz of B4 oplevert. Hieronder staat een tabel van alle specifieke frequenties met hun toonhoogte/ octaaf verhouding (nootnamen staan op de x-as en octaafnummers op de y-as).

https://www.seventhstring.com/resources/notefrequencies.html

Deze verzameling van ’twaalf noten per octaaf’ wordt de chromatische toonladder genoemd.Een ’toonladder’ is een verzameling noten in oplopende/aflopende volgorde beginnend/ eindigend op een fundamentele frequentie of toonhoogte. Een chromatische toonladder begint op een willekeurige toonhoogte en stijgt (of daalt) met 11 opeenvolgende halve stappen (halve tonen) vanaf de grondtoon. Op de bovenstaande grafiek kunt u de specifieke frequenties of noten/standen van elke chromatische toonladder vinden door te beginnen op een bepaalde noot (de grondtoon) en 11 halve tonen (aangrenzende toonhoogten) omhoog of omlaag te tellen.

Zoals u heeft gemerkt, zijn sommige noten in de bovenstaande grafiek ‘gespeld’ met een # (scherp) terwijl andere met een b (plat) zijn gespeld. Theoretisch kan elke noot een halve of hele stap/toon worden verhoogd of verlaagd door er een van deze symbolen achter te zetten. Er zijn echter conventies dat bepaalde noten op een bepaalde manier worden “gespeld”, gezien de gangbaarheid en voorspelbaarheid van de westerse muziektheoretische praktijk. Wat de “enharmonische schrijfwijzen” van noten en toonhoogten betreft (noten met dezelfde frequentie maar voorgesteld als verschillende toonhoogten), geeft bovenstaande tabel de meest voorkomende schrijfwijzen van noten en toonhoogten weer met betrekking tot de traditionele praktijken van “toonsoorten” in de muziek, maar bevat niet alle mogelijkheden. De volgende noten zijn veel voorkomende enharmonische schrijfwijzen (schuine strepen geven aan dat noten/pitches dezelfde frequentie hebben, maar als verschillende toonhoogtes kunnen worden voorgesteld of ‘gespeld’):

C#/Db D#/Eb F#/Gb G#/Ab A#/Bb

Natuurlijk kan theoretisch elke noot met een #- of b-symbool een halve (halve toon) of zelfs een hele (hele toon) stap worden verhoogd of verlaagd en in de wat meer geavanceerde muziektheorie komen de zogenaamde dubbelflats en -sharpen aan de orde.Zonder er al te ingewikkeld of diep op in te gaan, alle toonladders of muzikale toonaarden zijn een verzameling van halve stappen en hele stappen en de schrijfwijze van die toonhoogten geeft de uitvoerder aanwijzingen over de relaties (d.w.z. verhoudingen) tussen de toonhoogten die de componist gebruikt.

• Hertz (Hz)
• frequentie
• toon
• pitch
• A4 (A440)
• octaven
• gehele stappen (hele tonen)
• halve stappen (halve tonen)

Zelf-Quiz

• De toonhoogte G3 heeft een grondfrequentie van 196Hz. Zonder een tabel te raadplegen, wat zijn de frequenties van de toonhoogtes G2 en G4 (een octaaf onder en boven G4)?

Aanvullende hulpmiddelen