Laten we eens onderzoeken wat er gebeurt als negatieve waarden voorkomen onder het radicaalsymbool (als de radicand) voor kubuswortels en vierkantswortels.
In sommige situaties zijn negatieve getallen onder een radicaalsymbool OK. Zo is 
geen probleem omdat (-2) – (-2) – (-2) = -8, waardoor het antwoord -2 is. In kubiekwortelproblemen is het mogelijk een negatieve waarde driemaal met zichzelf te vermenigvuldigen en een negatief antwoord te krijgen.
Er ontstaan echter problemen wanneer we een probleem als 
bekijken. Dit vierkantswortelprobleem vraagt om een getal vermenigvuldigd met zichzelf dat een product (antwoord) van -16 oplevert. Er is gewoon geen manier om een getal met zichzelf te vermenigvuldigen en toch een negatief resultaat te krijgen. Overweeg: (4) – (4) = 16 en (-4) – (-4) = 16.
|
KubusHOEKEN:
 |
MAAR
|
VierkanteHOEKEN:
 |
|
Ja, (-2) x (-2) x (-2) = -8.
Geen probleem. |
Nee! (4) x (4) ≠ -16. |
Vierkantswortels zijn de boosdoeners! De moeilijkheden ontstaan wanneer je een negatieve waarde onder een vierkantswortel tegenkomt. Het is niet mogelijk om een waarde te kwadrateren (te vermenigvuldigen met zichzelf) en tot een negatieve waarde te komen. Wat doen we dan?
 |
De vierkantswortel van een negatief getal bestaat niet in de verzameling van reele getallen.
|
Toen problemen met negatieven onder een vierkantswortel voor het eerst opdoken, dachten wiskundigen dat er geen oplossing bestond. Zij zagen vergelijkingen als x2 + 1 = 0, en vroegen zich af wat de oplossing 
eigenlijk betekende.
In een poging dit probleem op te lossen, “creëerden” wiskundigen een nieuw getal, i, dat een “imaginair getal” werd genoemd, omdat het niet tot de verzameling “reële getallen” behoorde. Dit nieuwe getal werd met veel scepsis bekeken. Het imaginaire getal verscheen voor het eerst in druk in het jaar 1545.
 |
Het imaginaire getal “i” is de vierkantswortel van negatief één. |
Een imaginair getal bezit de unieke eigenschap dat wanneer het gekwadrateerd wordt, de uitkomst negatief is.
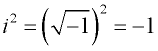
Bedenk: 
Het proces van vereenvoudigen van een radicaal dat een negatieve factor bevat, is hetzelfde als de normale radicaalvereenvoudiging. Het enige verschil is dat de 
wordt vervangen door een “i “.
Terwijl het onderzoek naar imaginaire getallen voortduurde, ontdekte men dat zij in feite een leemte in de wiskunde opvulden en een nuttig doel dienden. Imaginaire getallen zijn essentieel voor de studie van wetenschappen zoals elektriciteit, kwantummechanica, trillingsanalyse en cartografie.
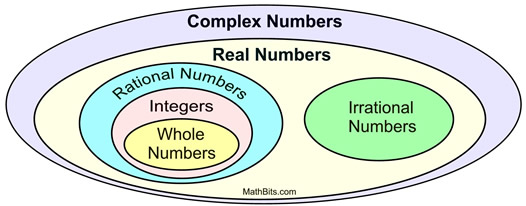
Toen de imaginaire i werd gecombineerd met de verzameling van reële getallen, werd de allesomvattende verzameling van complexe getallen gevormd.
