Identitatea lui Euler este o egalitate găsită în matematică care a fost comparată cu un sonet shakespearian și descrisă ca fiind „cea mai frumoasă ecuație”. Este un caz special al unei ecuații fundamentale în aritmetica complexă numită Formula lui Euler, pe care regretatul mare fizician Richard Feynman a numit-o în prelegerile sale „bijuteria noastră” și „cea mai remarcabilă formulă din matematică”.
Într-un interviu acordat BBC, profesorul David Percy de la Institutul de Matematică și Aplicațiile sale a declarat că Identitatea lui Euler este „un adevărat clasic și nu se poate face mai bine de atât … Este simplu de privit și totuși incredibil de profund, cuprinde cele mai importante cinci constante matematice.”
Identitatea lui Euler se scrie simplu ca: eiπ + 1 = 0
Cele cinci constante sunt:
- Numărul 0.
- Numărul 1.
- Numărul π, un număr irațional (cu cifre nesfârșite) care reprezintă raportul dintre circumferința unui cerc și diametrul său. Este aproximativ 3,14159…
- Numărul e, de asemenea un număr irațional. Este baza logaritmilor naturali care apare în mod natural prin studierea dobânzii compuse și a calculului. Numărul e pătrunde în matematică, apărând aparent de nicăieri într-un număr mare de ecuații importante. Este aproximativ 2,71828….
- Numărul i, definit ca fiind rădăcina pătrată a lui unu negativ: √(-1). Cel mai fundamental dintre numerele imaginare, denumit astfel deoarece, în realitate, niciun număr nu poate fi înmulțit cu el însuși pentru a produce un număr negativ (și, prin urmare, numerele negative nu au rădăcini pătrate reale). Dar, în matematică, există multe situații în care cineva este obligat să ia rădăcina pătrată a unui număr negativ. Prin urmare, litera i este folosită ca un fel de înlocuitor pentru a marca locurile în care s-a făcut acest lucru.
Matematician prolific
Leonhard Euler a fost un matematician de origine elvețiană din secolul al XVIII-lea care a dezvoltat multe concepte care fac parte integrantă din matematica modernă. Și-a petrecut cea mai mare parte a carierei în Sankt Petersburg, Rusia. A fost unul dintre cei mai prolifici matematicieni din toate timpurile, potrivit Academiei Navale a SUA (USNA), cu 886 de lucrări și cărți publicate. O mare parte din producția sa a venit în ultimele două decenii de viață, când era complet orb. A fost atât de multă muncă încât Academia din Sankt Petersburg a continuat să-i publice lucrările postum timp de peste 30 de ani.
Contribuțiile importante ale lui Euler includ Formula lui Euler și Teorema lui Euler, ambele putând avea semnificații diferite în funcție de context. Potrivit USNA, în mecanică, există „unghiurile lui Euler (pentru a specifica orientarea unui corp rigid), teorema lui Euler (conform căreia fiecare rotație are o axă), ecuațiile lui Euler pentru mișcarea fluidelor și ecuația lui Euler-Lagrange (care provine din calculul variațiilor).”
Înmulțirea numerelor complexe
Identitatea lui Euler provine în mod natural din interacțiunile numerelor complexe, care sunt numere compuse din două bucăți: un număr real și un număr imaginar; un exemplu este 4+3i. Numerele complexe apar într-o multitudine de aplicații, cum ar fi mecanica ondulatorie (un studiu din cadrul mecanicii cuantice) și proiectarea circuitelor care utilizează curent alternativ (o practică obișnuită în ingineria electrică). În plus, numerele complexe (și verii lor, numerele hipercomplexe) au o proprietate care le face deosebit de utile pentru studiul graficii computerizate, roboticii, navigației, dinamicii zborurilor și mecanicii orbitale: înmulțirea lor le face să se rotească. Această proprietate ne va ajuta să înțelegem raționamentul din spatele Identității lui Euler.
În exemplul de mai jos, cinci numere complexe sunt reprezentate pe planul complex și formează împreună o „formă de casă”. Planul complex este similar cu o dreaptă numerică, cu excepția faptului că este bidimensional. Direcția orizontală reprezintă numerele reale, iar axa verticală reprezintă numerele imaginare. Fiecare număr complex în formă de casă este înmulțit cu numărul complex 4+3i și redesenat (săgeată verde).
După cum se poate observa, înmulțirea cu 4+3i are ca rezultat dilatarea formei casei (creșterea ariei și îndepărtarea de originea 0+0i cu aceeași cantitate) și rotirea (înclinarea cu un anumit unghi). Pentru a arăta că acesta este exact efectul înmulțirii cu 4+3i, este prezentat și efectul măririi casei de cinci ori și al rotirii cu 36,9 grade (săgeată roșie). Se produce exact același efect.
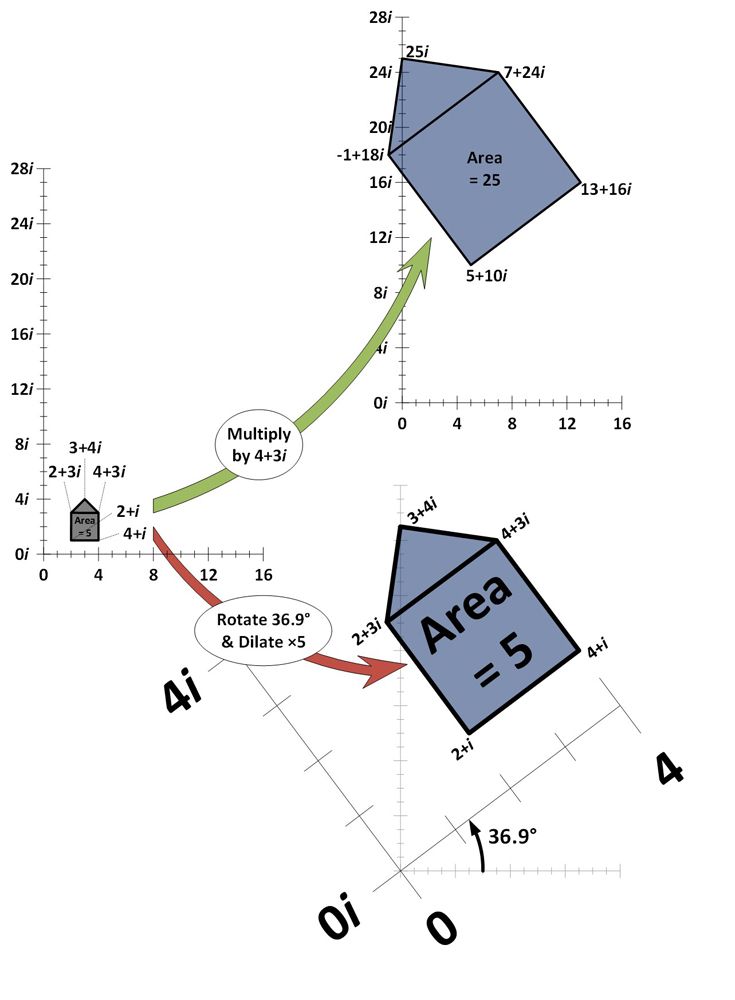
Diferite cantități de dilatare și rotație pot produce efectele înmulțirii cu orice număr din planul complex.
Forma polară a numerelor complexe
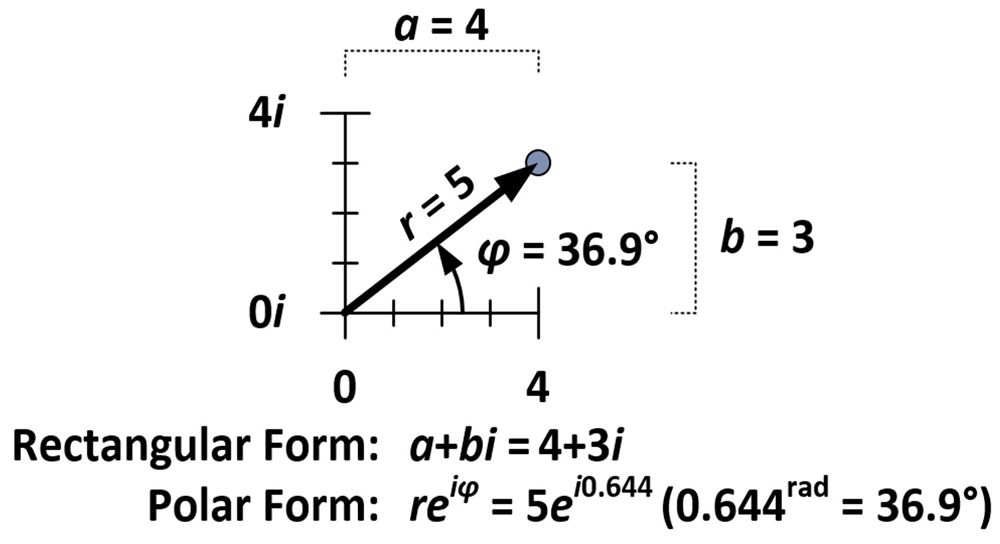
Cantitatea de rotație și dilatare este determinată de proprietăți intrinseci numărului 4+3i, care, așa cum se vede în figura de mai jos, se află la cinci unități de la origine (r = 5) și formează un unghi de 36,9 grade cu axa orizontală (φ = 36,9°). Aceste măsurători sunt utilizate în ceea ce se numește forma polară a unui număr complex (reiφ), spre deosebire de forma dreptunghiulară normală (a+bi).
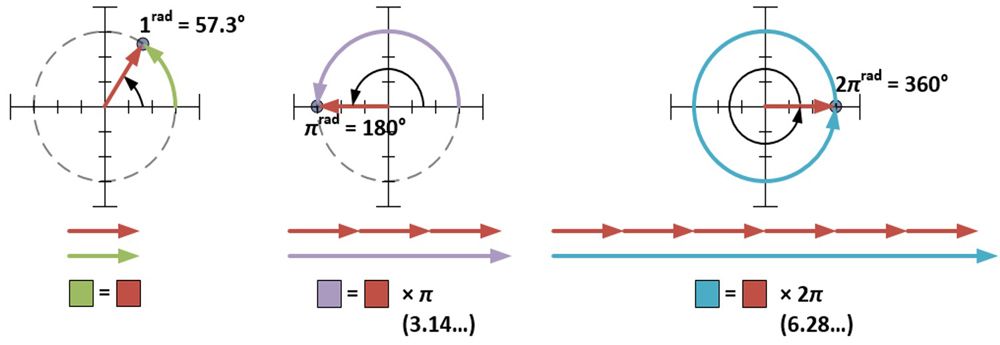
Forma polară necesită ca φ să fie măsurat în radiani. Un radian (1rad) reprezintă aproximativ 57,3 grade; este măsura unghiului format atunci când raza unui cerc este înfășurată pe circumferința acelui cerc. O măsură de π radiani înfășoară o jumătate de cerc; o măsură de 2π radiani înfășoară un cerc complet.
Măsura unghiului pentru 4+3i este de 0,644 radiani (36,9° = 0,644rad), ceea ce înseamnă că forma polară a lui 4+3i este 5ei0,644. Măsurile pentru r și φ pot fi, de asemenea, determinate pentru fiecare dintre punctele cu formă de casă și încă o altă modalitate de a obține efectul de dilatare/rotație al înmulțirii cu 4+3i este de a înmulți fiecare r cu cinci și de a adăuga 36,9 grade (sau 0,644rad) la fiecare φ. Din această demonstrație, vedem că, atunci când numerele complexe sunt înmulțite împreună, distanțele se înmulțesc și unghiurile se adună. Acest lucru se datorează unei proprietăți intrinseci exponenților, care poate fi demonstrată algebric.
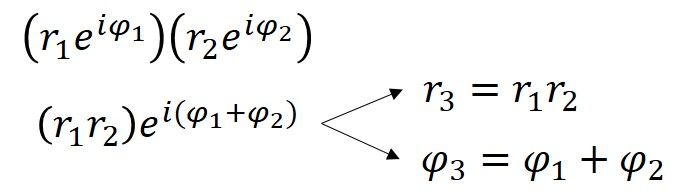
După stabilirea formei polare a numerelor complexe, chestiunea Identității lui Euler este doar un caz special de a+bi pentru a = -1 și b = 0. În consecință, pentru forma polară reiφ, aceasta face ca r = 1 și φ = π (deoarece πrad = 180°).
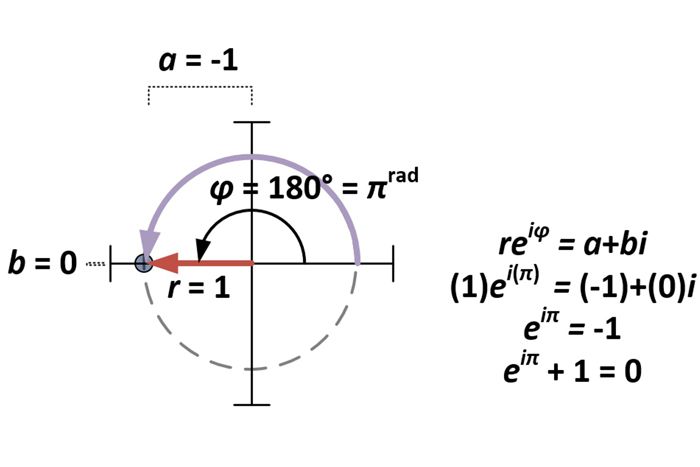
Derivarea formei polare
Deși Identitatea lui Euler rezultă din forma polară a numerelor complexe, este imposibil de derivat forma polară (în special apariția spontană a numărului e) fără calcul.
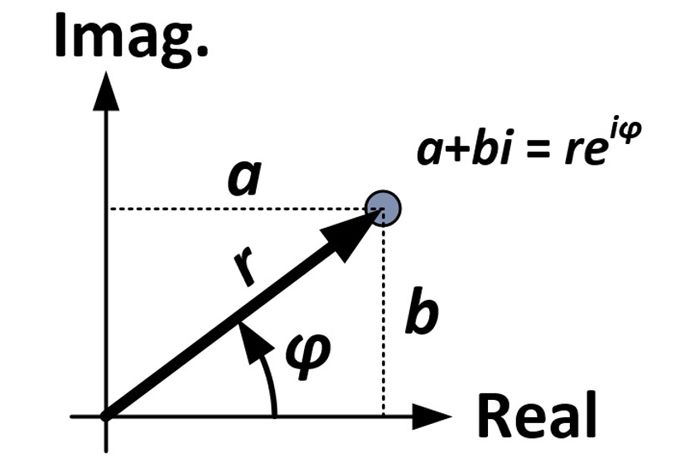
Începem cu forma dreptunghiulară a unui număr complex:
a + bi
Pe baza diagramei și a trigonometriei, putem face următoarele substituiri:
(r-cosφ) + (r-sinφ)i
De aici putem să factorizăm r:
r-(cosφ + i-sinφ)
Câteodată „cosφ + i-sinφ” este numit cisφ, care este o prescurtare pentru „cosinus plus sinus imaginar”.”
r-cisφ
Funcția cisφ se dovedește a fi egală cu eiφ. Aceasta este partea care este imposibil de arătat fără calcul. Două derivări sunt prezentate mai jos:

Așa, ecuația r-cisφ se scrie în forma polară standard r-eiφ.