Die Eulersche Identität ist eine Gleichung in der Mathematik, die mit einem Shakespeare-Sonett verglichen und als „die schönste Gleichung“ bezeichnet wurde. Sie ist ein Spezialfall einer grundlegenden Gleichung in der komplexen Arithmetik, der Eulerschen Formel, die der verstorbene große Physiker Richard Feynman in seinen Vorlesungen als „unser Juwel“ und „die bemerkenswerteste Formel der Mathematik“ bezeichnete.
In einem Interview mit der BBC sagte Prof. David Percy vom Institute of Mathematics and its Applications, die Eulersche Identität sei „ein echter Klassiker, und man kann es nicht besser machen … Sie ist einfach zu betrachten und doch unglaublich tiefgründig, sie umfasst die fünf wichtigsten mathematischen Konstanten.“
Die Eulersche Identität wird einfach geschrieben als: eiπ + 1 = 0
Die fünf Konstanten sind:
- Die Zahl 0.
- Die Zahl 1.
- Die Zahl π, eine irrationale Zahl (mit unendlichen Ziffern), die das Verhältnis des Umfangs eines Kreises zu seinem Durchmesser ist. Sie beträgt ungefähr 3,14159…
- Die Zahl e, ebenfalls eine irrationale Zahl. Sie ist die Basis der natürlichen Logarithmen, die sich auf natürliche Weise aus dem Studium der Zinseszinsen und der Infinitesimalrechnung ergibt. Die Zahl e durchdringt die Mathematik und taucht scheinbar aus dem Nichts in einer Vielzahl wichtiger Gleichungen auf. Sie ist ungefähr 2,71828….
- Die Zahl i, definiert als die Quadratwurzel aus minus eins: √(-1). Die grundlegendste der imaginären Zahlen, so genannt, weil in Wirklichkeit keine Zahl mit sich selbst multipliziert werden kann, um eine negative Zahl zu erhalten (und daher negative Zahlen keine realen Quadratwurzeln haben). In der Mathematik gibt es jedoch viele Situationen, in denen man gezwungen ist, die Quadratwurzel aus einer negativen Zahl zu ziehen. Der Buchstabe i wird daher als eine Art Ersatz verwendet, um die Stellen zu markieren, an denen dies geschehen ist.
Der berühmte Mathematiker
Leonhard Euler war ein in der Schweiz geborener Mathematiker des 18. Er verbrachte die meiste Zeit seiner Karriere in St. Petersburg, Russland. Nach Angaben der U.S. Naval Academy (USNA) war er einer der produktivsten Mathematiker aller Zeiten, der 886 Arbeiten und Bücher veröffentlichte. Ein Großteil seiner Arbeiten entstand in den letzten beiden Jahrzehnten seines Lebens, als er völlig erblindet war. Seine Arbeit war so umfangreich, dass die St. Petersburger Akademie seine Arbeiten noch mehr als 30 Jahre lang posthum veröffentlichte.
Zu Eulers wichtigen Beiträgen gehören die Eulersche Formel und das Eulersche Theorem, die beide je nach Kontext unterschiedliche Bedeutungen haben können. Laut USNA gibt es in der Mechanik „Euler-Winkel (zur Angabe der Ausrichtung eines starren Körpers), Eulers Theorem (dass jede Drehung eine Achse hat), Eulers Gleichungen für die Bewegung von Flüssigkeiten und die Euler-Lagrange-Gleichung (die aus der Variationsrechnung stammt).“
Multiplikation komplexer Zahlen
Die Eulersche Identität ergibt sich natürlich aus den Wechselwirkungen der komplexen Zahlen, die aus zwei Teilen bestehen: einer reellen Zahl und einer imaginären Zahl; ein Beispiel ist 4+3i. Komplexe Zahlen tauchen in einer Vielzahl von Anwendungen auf, z. B. in der Wellenmechanik (einer Untersuchung im Rahmen der Quantenmechanik) und beim Entwurf von Schaltkreisen, die Wechselstrom verwenden (eine gängige Praxis in der Elektrotechnik). Darüber hinaus haben komplexe Zahlen (und ihre Cousins, die hyperkomplexen Zahlen) eine Eigenschaft, die sie für die Untersuchung von Computergrafik, Robotik, Navigation, Flugdynamik und Orbitalmechanik besonders nützlich macht: Ihre Multiplikation bewirkt, dass sie sich drehen. Diese Eigenschaft wird uns helfen, die Überlegungen hinter der Eulerschen Identität zu verstehen.
Im folgenden Beispiel werden fünf komplexe Zahlen in der komplexen Ebene aufgetragen und bilden zusammen eine „Hausform“. Die komplexe Ebene ist ähnlich wie eine Zahlengerade, nur dass sie zweidimensional ist. Die horizontale Richtung steht für die reellen Zahlen und die vertikale Achse für die imaginären Zahlen. Jede komplexe Zahl in Hausform wird mit der komplexen Zahl 4+3i multipliziert und neu gezeichnet (grüner Pfeil).
Wie man sieht, führt die Multiplikation mit 4+3i dazu, dass sich die Hausform ausdehnt (die Fläche vergrößert sich und entfernt sich um den gleichen Betrag vom Ursprung 0+0i) und dreht (sie wird um einen bestimmten Winkel geneigt). Um zu zeigen, dass dies genau die Wirkung der Multiplikation mit 4+3i ist, wird auch die Wirkung einer fünffachen Vergrößerung des Hauses und einer Drehung um 36,9 Grad gezeigt (roter Pfeil). Es entsteht genau derselbe Effekt.
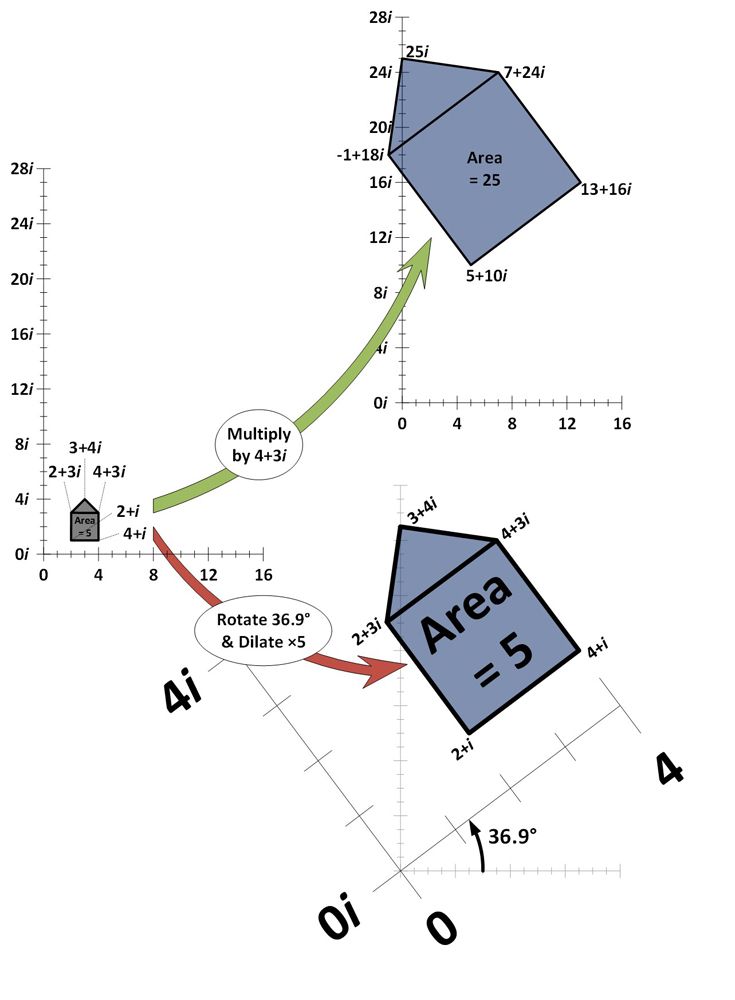
Unterschiedliche Dehnungs- und Rotationsbeträge können die Wirkung der Multiplikation mit einer beliebigen Zahl in der komplexen Ebene erzeugen.
Polare Form der komplexen Zahlen
Das Ausmaß der Rotation und Dilatation wird durch die Eigenschaften der Zahl 4+3i bestimmt, die, wie in der Abbildung unten zu sehen, fünf Einheiten vom Ursprung entfernt ist (r = 5) und einen Winkel von 36,9 Grad mit der horizontalen Achse bildet (φ = 36,9°). Diese Maße werden in der so genannten Polarform einer komplexen Zahl (reiφ) im Gegensatz zur normalen Rechteckform (a+bi) verwendet.
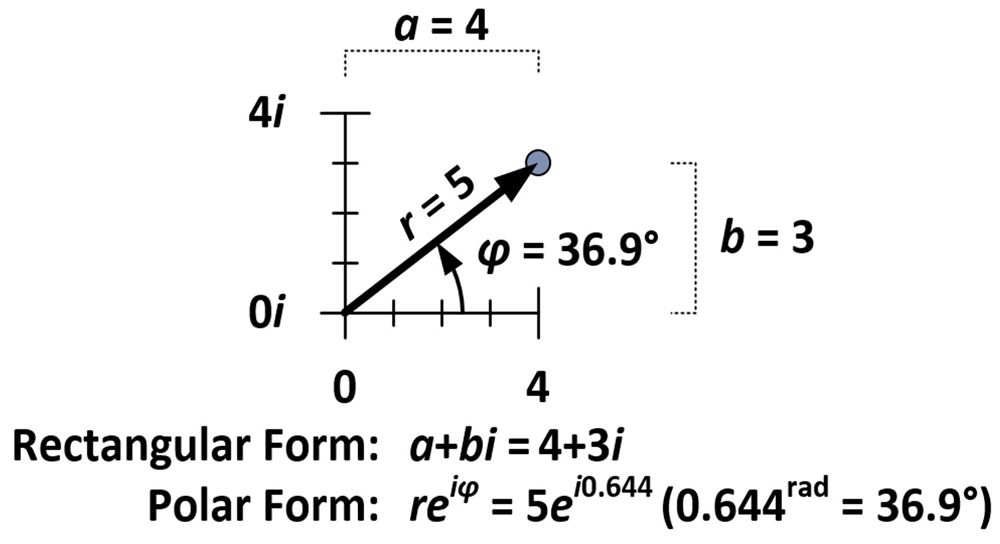
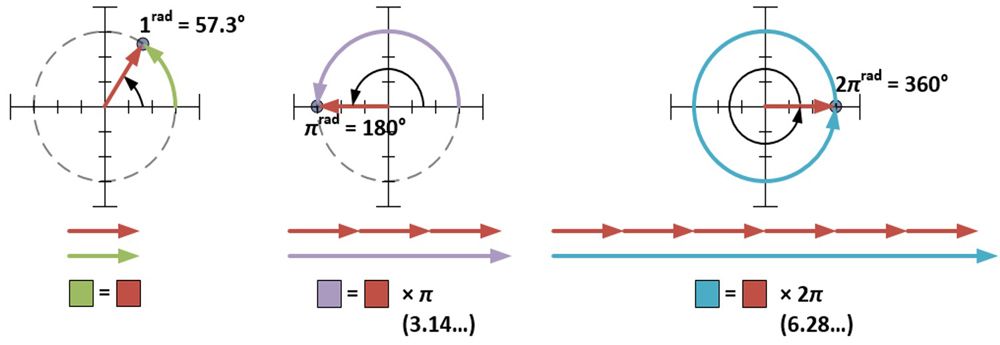
Die Polarform erfordert, dass φ in Radiant gemessen wird. Ein Bogenmaß (1rad) entspricht etwa 57,3 Grad; es ist das Maß des Winkels, der entsteht, wenn der Radius eines Kreises gegen den Umfang des Kreises gewickelt wird. Ein Maß von π Bogenmaß umschließt einen halben Kreis; ein Maß von 2π Bogenmaß umschließt einen ganzen Kreis.
Das Winkelmaß für 4+3i ist 0,644 Bogenmaß (36,9° = 0,644rad), was bedeutet, dass die Polarform von 4+3i 5ei0,644 ist. Die Maße für r und φ können auch für jeden der hausförmigen Punkte bestimmt werden, und eine weitere Möglichkeit, den dilatierenden/rotierenden Effekt der Multiplikation mit 4+3i zu erreichen, besteht darin, jedes r mit fünf zu multiplizieren und 36,9 Grad (oder 0,644rad) zu jedem φ hinzuzufügen. Aus dieser Demonstration geht hervor, dass sich bei der Multiplikation komplexer Zahlen Abstände multiplizieren und Winkel addieren. Dies ist auf eine den Exponenten innewohnende Eigenschaft zurückzuführen, die algebraisch gezeigt werden kann.
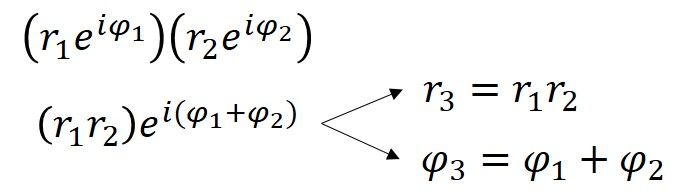
Mit der Polarform der komplexen Zahlen ist die Frage der Eulerschen Identität lediglich ein Spezialfall von a+bi für a = -1 und b = 0. Für die Polarform reiφ ergibt sich daraus r = 1 und φ = π (da πrad = 180°).
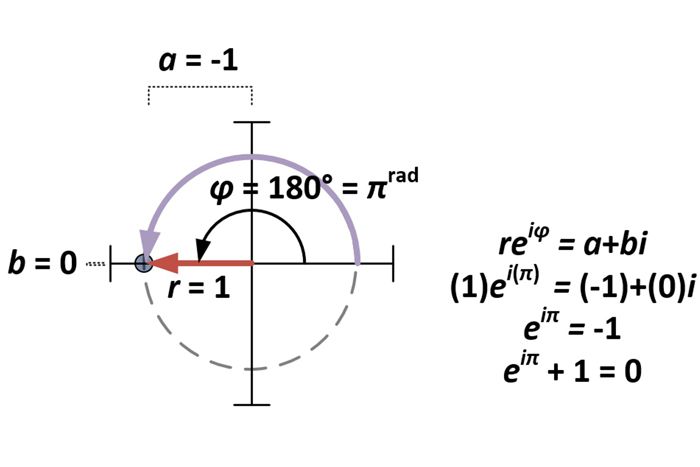
Ableitung der Polarform
Obwohl die Eulersche Identität aus der Polarform der komplexen Zahlen folgt, ist es unmöglich, die Polarform (insbesondere das spontane Auftreten der Zahl e) ohne Kalkül abzuleiten.
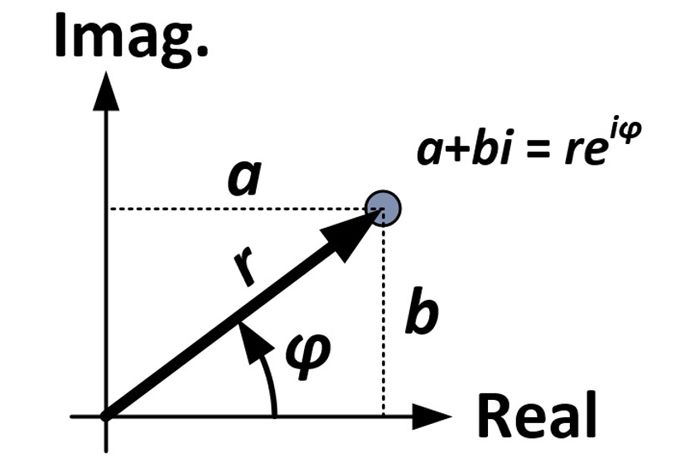
Wir beginnen mit der rechtwinkligen Form einer komplexen Zahl:
a + bi
Aus dem Diagramm und der Trigonometrie können wir die folgenden Ersetzungen vornehmen:
(r-cosφ) + (r-sinφ)i
Von hier aus können wir r faktorisieren:
r-(cosφ + i-sinφ)
Manchmal wird „cosφ + i-sinφ“ als cisφ bezeichnet, was eine Abkürzung für „Kosinus plus imaginärer Sinus“ ist.“
r-cisφ
Die Funktion cisφ stellt sich als gleich eiφ heraus. Das ist der Teil, den man ohne Kalkül nicht zeigen kann. Zwei Ableitungen werden unten gezeigt:

So wird die Gleichung r-cisφ in der Standard-Polarform r-eiφ geschrieben.