Qu’est-ce que la fréquence ? La fréquence est « la fréquence » à laquelle quelque chose se produit. Puisque le son est constitué de vibrations, nous utilisons la fréquence pour décrire la fréquence à laquelle quelque chose vibre.La fréquence est mesurée en Hertz (Hz), qui est simplement « la fréquence par seconde ».Ainsi, quelque chose qui oscille à 1 Hz vibre une fois par seconde. Une vibration « complète » s’appelle un « cycle », mesuré à un pic et un creux complets d’une onde (c’est-à-dire la distance maximale ou « amplitude » au-dessus du point central ou « 0 », représenté sur l’axe des x). (Au début de la musique électronique, les termes « cycles par seconde » étaient utilisés au lieu de Hz, que vous pouvez voir sur de nombreux synthétiseurs anciens/vintage aujourd’hui).
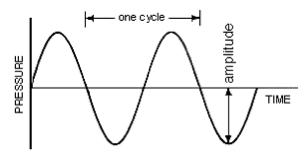
L’image ci-dessus est une onde sinusoïdale – la représentation la plus pure d’une seule fréquence ou vibration. Le temps qu’il faut à l’onde pour accomplir un cycle est la fréquence de l’onde (encore une fois, « à quelle fréquence » elle vibre). Plus de vibrations par seconde (c’est-à-dire des oscillations plus rapides) produisent des fréquences sonores « élevées » et moins de vibrations par seconde (c’est-à-dire des oscillations plus lentes) produisent des fréquences sonores « basses ». L’être humain ne peut entendre que des fréquences comprises approximativement entre 20 Hz et 20 000 Hz (20 kHz) (pour en savoir plus, voir https://en.wikipedia.org/wiki/Hearing_range).
En musique, les termes fréquence, hauteur et ton sont liés.Un ton est un son ayant une ou plusieurs fréquences identifiables. La fréquence est la mesure empirique d’un phénomène physique, définie comme le nombre de cycles (de vibration) par seconde. La hauteur est une perception subjective de la hauteur relative d’un son, comme dans « haut » ou « bas » (pour en savoir plus, voir Conceptual Modelsand Cross-Domain Mapping de Lawerence Zbikowskihttp://zbikowski.uchicago.edu/pdfs/ZbikowskiConceptualmodels_1997.pdf).
Alors que les fréquences sont représentées par des chiffres (Hz), la hauteur est représentée par des lettres. Par exemple, si vous avez déjà entendu un orchestre » s’accorder » au début d’un concert, un seul joueur (généralement un hautbois ou un violon) joue un » la » mesuré à 440 Hz (appelé A440). En ce qui concerne la hauteur des sons, nous n’utilisons que les lettres A, B, C, D, E, F et G (des symboles supplémentaires sont utilisés pour les élever ou les abaisser, nous y reviendrons plus tard). Ces hauteurs se répètent toutes les 8 notes, appelées octaves. Afin de différencier les octaves auxquelles nous nous référons lorsque nous parlons de hauteur, un chiffre est ajouté après la lettre. Par exemple, A440(Hz)est appelé A4 en termes de hauteur. Ne vous méprenez pas, le 4 fait référence à l’octave dans laquelle nous nous référons à ce la particulier (spécifiquement au piano) – c’est juste une coïncidence que la fréquence soit 440, le 4 ne fait pas spécifiquement référence à cela. Mais pourquoi A4 est-il 440 Hz, me direz-vous ? Eh bien, il y a une réponse assez compliquée à cette question, mais en fin de compte, c’est effectivement arbitraire. Pour faire simple, un groupe de personnes s’est réuni au 19ème siècle et a décidé que c’était le cas. (Si vous souhaitez en savoir plus sur le sujet, faites des recherches sur A440 ou sur les normes de hauteur/accordhttps://en.wikipedia.org/wiki/A440(pitchstandard)).
Il est important de noter que la fréquence est absolue, alors que la hauteur est relative(ces changements relatifs sont appelés « accord »). Nous utilisons les hauteurs pour décrire leur relation (c’est-à-dire leur rapport) avec d’autres hauteurs et l’analyse de ces relations est la base de la « théorie musicale ». En général, nous avons convenu que A4 est défini comme la hauteur dont la fréquence est de 440 Hz (une référence absolue). Nous pouvons ensuite déterminer la « hauteur » ou « l’accord » de toutes les autres notes par rapport à cela en utilisant une formule d’accord particulière.
Un aspect très important de toute la théorie musicale est que les octaves sont spécifiquement définies comme « doublant » ou « divisant par deux » la fréquence d’une hauteur. Par exemple, les fréquences 220 Hz, 440 Hz, et 880 Hz sont toutes des A, mais existent dans des octaves différentes : A3, A4, et A5 respectivement. Dans la théorie de la musique occidentale, nous avons généralement (et franchement, arbitrairement) convenu que dans chaque octave, il y a 12 subdivisions ou hauteurs égales. Alors comment déterminer où ces autres notes sont « accordées » par rapport à cette A440 ? Eh bien, après de nombreuses années d’expérimentation, il a été décidé que la formule suivante détermine la relation relative entre les hauteurs (plus précisément, la fréquence f de la nième touche d’un piano standard):
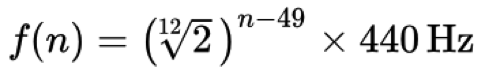https://en.wikipedia.org/wiki/Pianokeyfrequencies
En termes simples, chaque ton/taille dans l’accord de la musique classique occidentale est dérivé en commençant par A440 comme « ton de référence », puis en multipliant ou en divisant par la douzième racine de deux (~1,059463) pour obtenir un autre ton au-dessus ou au-dessous de ce ton de référence. Le nombre 49 dans ce cas est arbitraire (A4 est la 49e touche sur un clavier de piano standard) et dans la musique assistée par ordinateur, nous utilisons généralement les numéros MIDI pour nos calculs – A440 est la touche MIDI numéro 69 par exemple (plus d’informations sur les normes MIDI dans une autre leçon).
Il convient de noter que cette formule ne représente qu’un style particulier d' »accordage » qui existe dans la tradition de la musique classique occidentale et qui est utilisé en général comme « norme mondiale » lorsqu’on parle des relations hauteur/fréquence/ton en général, même si ces relations sont arbitraires et que d’autres systèmes d’accordage existent dans différentes cultures et traditions.Ce système conserve une « règle » importante selon laquelle les octaves sont définies comme le doublement ou la réduction exacte des fréquences tout en conservant les mêmes rapports (de hauteur) de division de chaque octave en 12 parties égales. Nous appelons ce système d’accordage le tempérament égal à 12 tons et il sert de base à la plupart des pays du monde en tant que système d’accordage fondamental et convenu, en particulier lorsqu’il s’agit de la normalisation des équipements musicaux électroniques. (Tous les pianos sont accordés selon ce système et toutes les données MIDI suivent ce principe général).
Dans la terminologie musicale, nous décrivons les hauteurs (ou tons) comme ascendantes ou descendantes en termes de « pas ». Il existe deux types de pas :les demi-pas et les pas entiers (également appelés demi-tons ou tons entiers).L’élévation des notes d’un demi-pas (c’est-à-dire un demi-ton) est indiquée par un symbole ♯ appelé » dièse » (symbole numérique ou hashtag) et l’abaissement des tons d’un demi-pas est indiqué par un symbole ♭ appelé » bémol » (un » b » minuscule est également fréquemment utilisé). Vous pouvez considérer les demi-tons ou les demi-pas comme la distance minimale entre deux touches de piano ou frettes de guitare adjacentes.
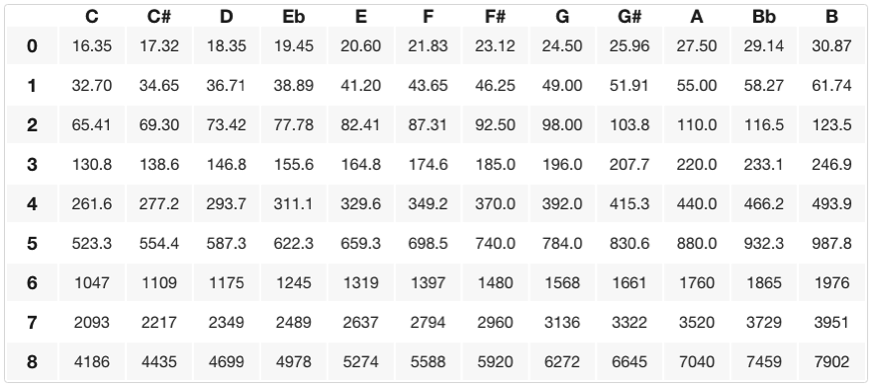
Pour obtenir la fréquence d’un demi-ton au-dessus de A4, nous multiplions 440 Hz par la douzième racine de deux pour obtenir ~466,2 Hz, ce qui nous donne un A# (ou un Bb). Le la# et le si sont appelés des « notes enharmoniques », ou des hauteurs qui sont techniquement de la même fréquence mais qui peuvent être « épelées » différemment selon la « clé » ou le contexte musical dont nous parlons (plus d’informations à ce sujet dans une autre leçon). Pour obtenir la fréquence d’un cran au-dessus de A4, nous pouvons multiplier deux fois 440Hz par la douzième racine de deux, ce qui nous donne ~493,9 Hz ou B4. Ci-dessous se trouve un tableau de toutes les fréquences spécifiques avec leur relation hauteur/octave (les noms des notes sont sur l’axe des x et les numéros d’octave sont sur l’axe des y).
https://www.seventhstring.com/resources/notefrequencies.html
Cette collection de ‘douze notes par octave’ est appelée la gamme chromatique.Une ‘gamme’ est une collection de notes en ordre croissant/décroissant commençant/finissant sur une fréquence ou hauteur fondamentale. Une gamme chromatique commence sur n’importe quelle hauteur et monte (ou descend) de 11 demi-pas adjacents successifs (demi-tons) à partir de sa fondamentale. Sur le tableau ci-dessus, vous pouvez trouver les fréquences ou notes/pitchs spécifiques de toute échelle chromatique en commençant sur une note donnée (la fondamentale) et en comptant vers le haut ou vers le bas 11 demi-tons(pitchs adjacents).
Si vous avez remarqué, certaines des notes du tableau ci-dessus sont « épelées » avec un #(dièse) tandis que d’autres sont épelées avec un b (bémol). Théoriquement, toute note peut être élevée ou abaissée d’un demi-ton ou d’un ton entier en ajoutant l’un de ces symboles après elle. Cependant, il existe des conventions selon lesquelles certaines notes sont « épelées » d’une manière particulière étant donné la prévalence et la prévisibilité des pratiques théoriques de la musique occidentale. En ce qui concerne les « graphies enharmoniques » des notes et des hauteurs (notes de même fréquence mais représentées par des hauteurs différentes), le tableau ci-dessus représente les graphies les plus courantes des notes et des hauteurs au regard des pratiques traditionnelles des « signatures de clé » en musique, mais n’inclut pas toutes les possibilités. Les notes suivantes sont des épellations enharmoniques courantes (les barres obliques indiquent que les notes/pic sont de même fréquence mais peuvent être représentées ou » épelées » comme des hauteurs différentes) :
C#/Db D#/Eb F#/Gb G#/Ab A#/Bb
Bien sûr, théoriquement, n’importe quelle note peut être élevée ou abaissée d’un demi-ton ou même d’un ton entier avec un symbole # ou b. Un peu plus avancé dans la théorie musicale, on parle de double bémol et de dièse.Sans entrer dans les détails, toutes les gammes ou clés musicales sont une collection de demi-pas et de pas entiers et l’orthographe de ces hauteurs donne à l’interprète des indices sur les relations (c’est-à-dire les rapports) entre les hauteurs utilisées par le compositeur.
- Hertz (Hz)
- fréquence
- tone
- pitch
- A4 (A440)
- octaves
- pas entiers (tons entiers)
- demi-pas (demi-tons)
Self-Quiz
- Le diapason G3 a une fréquence fondamentale de 196Hz. Sans consulter une table, quelles sont les fréquences des hauteurs G2 et G4 (une octave en dessous et au-dessus de G4) ?
Ressources supplémentaires
- Propriétés du son – Khan Academy
- Son : Cours accéléré de physique
.