L’identità di Eulero è un’uguaglianza trovata in matematica che è stata paragonata a un sonetto shakespeariano e descritta come “la più bella equazione”. È un caso speciale di un’equazione fondamentale dell’aritmetica complessa chiamata Formula di Eulero, che il grande fisico Richard Feynman ha chiamato nelle sue conferenze “il nostro gioiello” e “la formula più notevole della matematica”.
In un’intervista con la BBC, il Prof David Percy dell’Istituto di Matematica e delle sue Applicazioni ha detto che l’Identità di Eulero è “un vero classico e non si può fare meglio di così … È semplice da guardare e tuttavia incredibilmente profondo, comprende le cinque costanti matematiche più importanti.”
L’identità di Eulero si scrive semplicemente come: eiπ + 1 = 0
Le cinque costanti sono:
- Il numero 0.
- Il numero 1.
- Il numero π, un numero irrazionale (con cifre infinite) che è il rapporto tra la circonferenza di un cerchio e il suo diametro. È circa 3,14159…
- Il numero e, anch’esso un numero irrazionale. È la base dei logaritmi naturali che nasce naturalmente dallo studio dell’interesse composto e del calcolo. Il numero e pervade la matematica, apparendo apparentemente dal nulla in un gran numero di equazioni importanti. È circa 2,71828….
- Il numero i, definito come la radice quadrata di uno negativo: √(-1). Il più fondamentale dei numeri immaginari, così chiamato perché, in realtà, nessun numero può essere moltiplicato per se stesso per produrre un numero negativo (e, quindi, i numeri negativi non hanno radici quadrate reali). Ma in matematica, ci sono molte situazioni in cui si è costretti a prendere la radice quadrata di un negativo. La lettera i è quindi usata come una sorta di controfigura per segnare i luoghi in cui questo è stato fatto.
Matematico prolifico
Leonhard Euler era un matematico svizzero del XVIII secolo che ha sviluppato molti concetti che sono parte integrante della matematica moderna. Ha trascorso la maggior parte della sua carriera a San Pietroburgo, in Russia. È stato uno dei matematici più prolifici di tutti i tempi, secondo l’Accademia Navale degli Stati Uniti (USNA), con 886 articoli e libri pubblicati. Gran parte della sua produzione è avvenuta negli ultimi due decenni della sua vita, quando era totalmente cieco. C’era così tanto lavoro che l’Accademia di San Pietroburgo continuò a pubblicare il suo lavoro postumo per più di 30 anni.
I contributi importanti di Eulero includono la Formula di Eulero e il Teorema di Eulero, entrambi i quali possono significare cose diverse a seconda del contesto. Secondo l’USNA, in meccanica, ci sono “gli angoli di Eulero (per specificare l’orientamento di un corpo rigido), il teorema di Eulero (che ogni rotazione ha un asse), le equazioni di Eulero per il moto dei fluidi e l’equazione di Eulero-Lagrange (che deriva dal calcolo delle variazioni).”
Moltiplicando i numeri complessi
L’identità di Eulero deriva naturalmente dalle interazioni dei numeri complessi che sono numeri composti da due parti: un numero reale e un numero immaginario; un esempio è 4+3i. I numeri complessi appaiono in una moltitudine di applicazioni come la meccanica delle onde (uno studio all’interno della meccanica quantistica) e la progettazione di circuiti che utilizzano la corrente alternata (una pratica comune in ingegneria elettrica). Inoltre, i numeri complessi (e i loro cugini, i numeri ipercomplessi) hanno una proprietà che li rende particolarmente utili per lo studio della computer grafica, della robotica, della navigazione, della dinamica del volo e della meccanica orbitale: moltiplicandoli tra loro, essi ruotano. Questa proprietà ci aiuterà a capire il ragionamento dietro l’identità di Eulero.
Nell’esempio qui sotto, cinque numeri complessi sono tracciati sul piano complesso e insieme formano una “forma di casa”. Il piano complesso è simile a una linea dei numeri, tranne che è bidimensionale. La direzione orizzontale rappresenta i numeri reali e l’asse verticale rappresenta i numeri immaginari. Ogni numero complesso a forma di casa viene moltiplicato per il numero complesso 4+3i e ridisegnato (freccia verde).
Come si può vedere, moltiplicando per 4+3i la forma della casa si dilata (aumentando l’area e allontanandosi dall’origine 0+0i della stessa quantità) e ruota (diventando inclinata di qualche angolo). Per mostrare che questo è esattamente l’effetto della moltiplicazione per 4+3i, viene mostrato anche l’effetto dello zoom sulla casa cinque volte e della rotazione di 36,9 gradi (freccia rossa). Si produce esattamente lo stesso effetto.
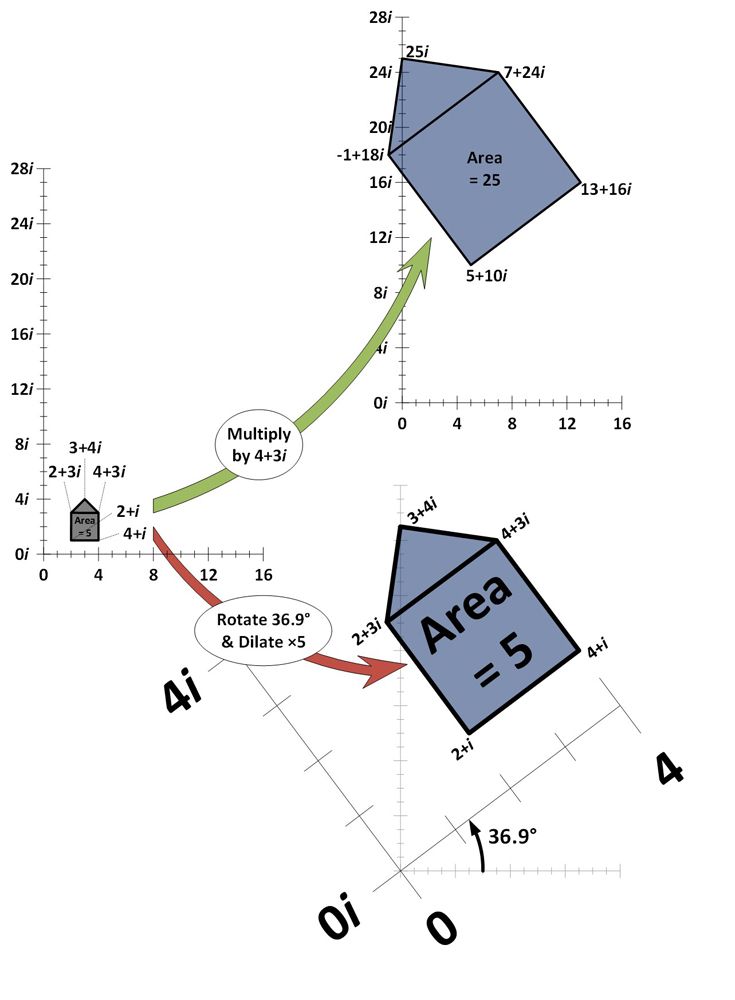
Diverse quantità di dilatazione e rotazione possono produrre gli effetti della moltiplicazione per qualsiasi numero sul piano complesso.
Forma polare dei numeri complessi
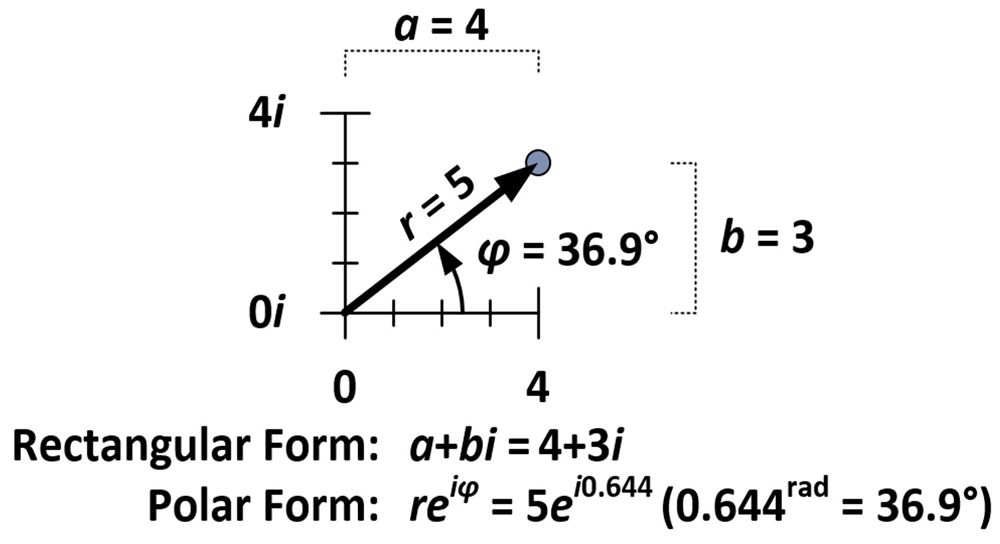
La quantità di rotazione e dilatazione è determinata da proprietà intrinseche al numero 4+3i, che, come si vede nella figura qui sotto, è a cinque unità dall’origine (r = 5) e forma un angolo di 36,9 gradi con l’asse orizzontale (φ = 36,9°). Queste misure sono usate in quella che è conosciuta come la forma polare di un numero complesso (reiφ) in opposizione alla normale forma rettangolare (a+bi).
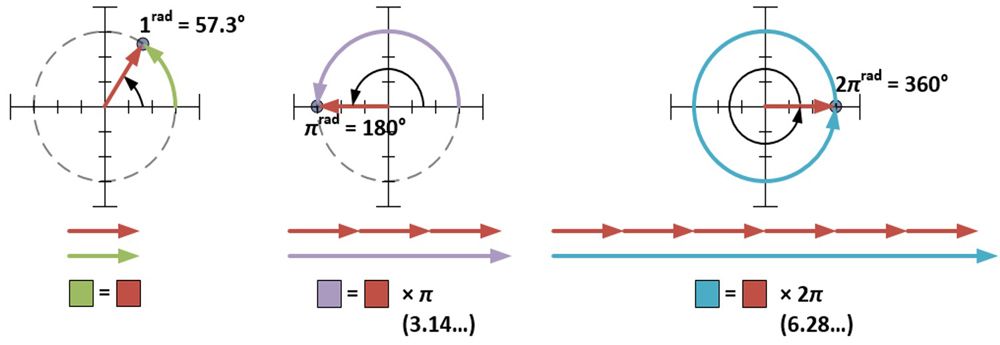
La forma polare richiede che φ sia misurata in radianti. Un radiante (1rad) è approssimativamente 57,3 gradi; è la misura dell’angolo fatto quando il raggio di un cerchio è avvolto contro la circonferenza di quel cerchio. Una misura di π radianti avvolge metà di un cerchio; una misura di 2π radianti avvolge un cerchio completo.
La misura dell’angolo per 4+3i è 0,644 radianti (36,9° = 0,644rad) che significa che la forma polare di 4+3i è 5ei0,644. Le misure di r e φ possono anche essere determinate per ciascuno dei punti della forma della casa, e un altro modo per ottenere l’effetto dilatante/rotante della moltiplicazione per 4+3i è quello di moltiplicare ogni r per cinque, e aggiungere 36,9 gradi (o 0,644rad) a ogni φ. Da questa dimostrazione, vediamo che quando i numeri complessi sono moltiplicati insieme, le distanze si moltiplicano e gli angoli si aggiungono. Questo è dovuto a una proprietà intrinseca agli esponenti, che può essere dimostrata algebricamente.
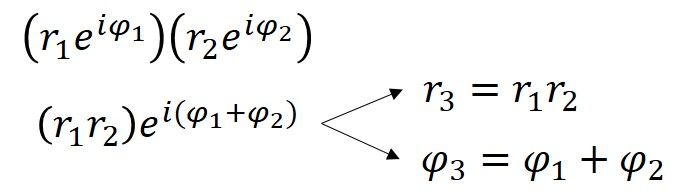
Con la forma polare dei numeri complessi stabilita, la questione dell’identità di Eulero è semplicemente un caso speciale di a+bi per a = -1 e b = 0. Di conseguenza, per la forma polare reiφ, questo fa r= 1 e φ = π (poiché πrad = 180°).
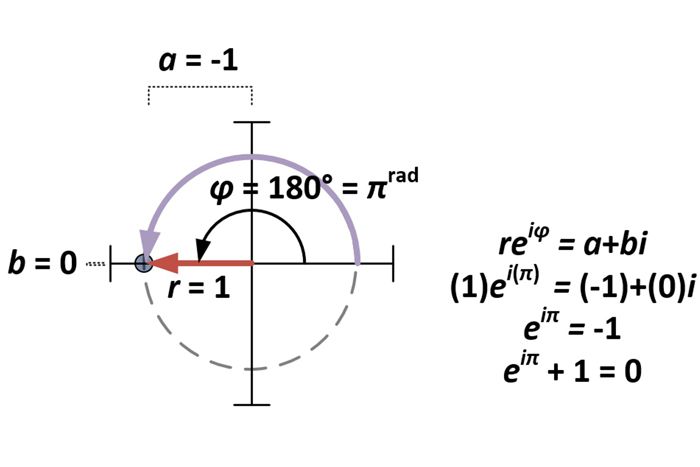
Derivazione della forma polare
Anche se l’Identità di Eulero segue dalla forma polare dei numeri complessi, è impossibile derivare la forma polare (in particolare l’aspetto spontaneo del numero e) senza calcolo.
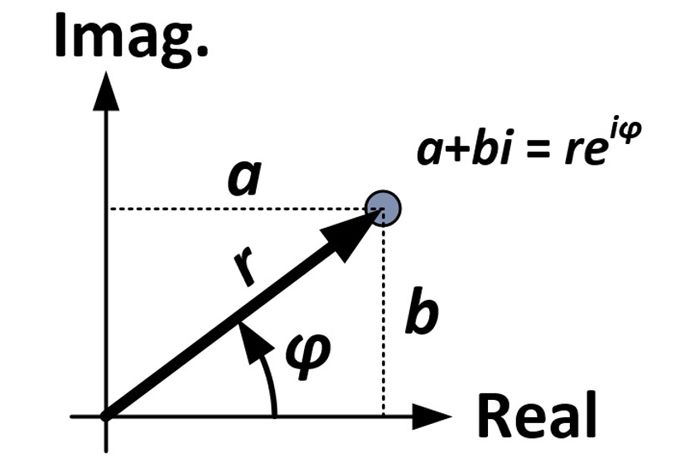
Partiamo dalla forma rettangolare di un numero complesso:
a + bi
Dal diagramma e dalla trigonometria, possiamo fare le seguenti sostituzioni:
(r-cosφ) + (r-sinφ)i
Da qui possiamo fattorizzare r:
r-(cosφ + i-sinφ)
A volte “cosφ + i-sinφ” è chiamato cisφ, che è un’abbreviazione di “coseno più seno immaginario.”
r-cisφ
La funzione cisφ risulta essere uguale a eiφ. Questa è la parte che è impossibile da mostrare senza calcoli. Due derivazioni sono mostrate qui sotto:

Quindi, l’equazione r-cisφ è scritta nella forma polare standard r-eiφ.