Eulers identitet: ”Den vackraste ekvationen”

Eulers identitet är en jämlikhet inom matematiken som har jämförts med en sonett från Shakespeare och beskrivits som ”den vackraste ekvationen”. Det är ett specialfall av en grundläggande ekvation i komplex aritmetik som kallas Eulers formel, som den framlidne store fysikern Richard Feynman i sina föreläsningar kallade ”vår juvel” och ”den mest anmärkningsvärda formeln i matematiken”.

I en intervju med BBC sade professor David Percy från Institute of Mathematics and its Applications att Eulers identitet var ”en riktig klassiker och man kan inte göra det bättre än så … Den är enkel att se på och ändå otroligt djupgående, den omfattar de fem viktigaste matematiska konstanterna.”

Eulers identitet skrivs enkelt som: eiπ + 1 = 0

De fem konstanterna är:

• Talet 0.
• Talet 1.
• Talet π, ett irrationellt tal (med oändliga siffror) som är förhållandet mellan en cirkels omkrets och dess diameter. Det är ungefär 3,14159…
• Talet e, som också är ett irrationellt tal. Det är basen för naturliga logaritmer som uppstår naturligt genom studier av sammansatt ränta och kalkyl. Talet e genomsyrar matematiken och dyker upp till synes från ingenstans i ett stort antal viktiga ekvationer. Det är ungefär 2,71828….
• Talet i, definierat som kvadratroten av negativt ett: √(-1). Det mest grundläggande av de imaginära talen, som kallas så eftersom inget tal i verkligheten kan multipliceras med sig självt för att ge ett negativt tal (och därför har negativa tal inga verkliga kvadratrötter). Men inom matematiken finns det många situationer där man tvingas ta kvadratroten av ett negativt tal. Bokstaven i används därför som ett slags stand-in för att markera platser där detta har gjorts.

Prolificerande matematiker

Leonhard Euler var en schweiziskfödd matematiker från 1700-talet som utvecklade många begrepp som är en integrerad del av den moderna matematiken. Han tillbringade större delen av sin karriär i S:t Petersburg i Ryssland. Han var en av de mest produktiva matematikerna genom tiderna, enligt U.S. Naval Academy (USNA), med 886 publicerade artiklar och böcker. En stor del av hans produktion kom under de två sista decennierna av hans liv, då han var helt blind. Det var så mycket arbete att St Petersburg Academy fortsatte att publicera hans arbete postumt i mer än 30 år.

Eulers viktiga bidrag inkluderar Eulers formel och Eulers sats, som båda kan betyda olika saker beroende på sammanhanget. Enligt USNA finns det inom mekaniken ”Eulers vinklar (för att ange orienteringen av en stel kropp), Eulers sats (att varje rotation har en axel), Eulers ekvationer för vätskors rörelse och Euler-Lagrange-ekvationen (som kommer från variationskalkylen).”

Multiplicering av komplexa tal

Eulers identitet härrör naturligt från interaktioner av komplexa tal som är tal som består av två delar: ett reellt tal och ett imaginärt tal; ett exempel är 4+3i. Komplexa tal förekommer i en mängd olika tillämpningar, t.ex. vågmekanik (en studie inom kvantmekaniken) och utformning av kretsar som använder växelström (en vanlig metod inom elektroteknik). Dessutom har komplexa tal (och deras kusiner, de hyperkomplexa talen) en egenskap som gör dem särskilt användbara för studier av datorgrafik, robotteknik, navigering, flygdynamik och banmekanik: om man multiplicerar dem tillsammans roterar de. Denna egenskap hjälper oss att förstå resonemanget bakom Eulers identitet.

I exemplet nedan ritas fem komplexa tal in på det komplexa planet och bildar tillsammans en ”husform”. Det komplexa planet liknar en tallinje, förutom att det är tvådimensionellt. Den horisontella riktningen representerar de reella talen och den vertikala axeln representerar de imaginära talen. Varje husformigt komplext tal multipliceras med det komplexa talet 4+3i och ritas in på nytt (grön pil).

Som framgår resulterar multiplikationen med 4+3i i att husformen utvidgas (ökar i area och rör sig lika mycket bort från origo 0+0i) och roterar (blir lutande i en viss vinkel). För att visa att detta är just effekten av att multiplicera med 4+3i visas också effekten av att zooma in på huset fem gånger och rotera 36,9 grader (röd pil). Exakt samma effekt uppnås.

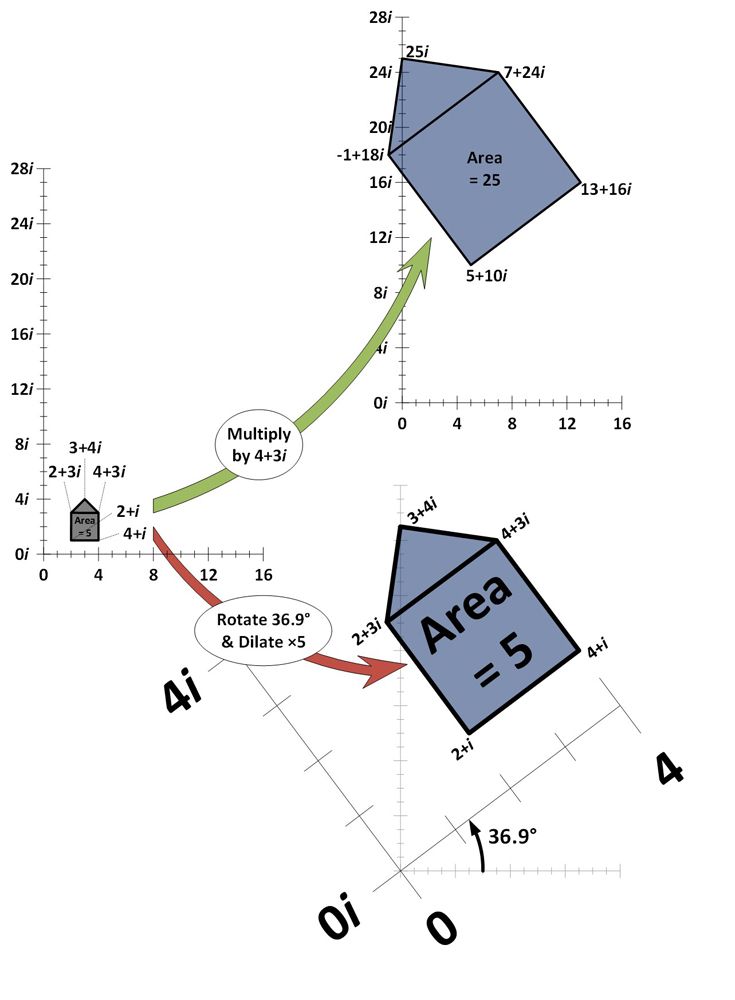
Differentierade mängder utbredning och rotation kan ge effekten av att multiplicera med vilket tal som helst på det komplexa planet.

Komplexa tals polarform

Mängden rotation och dilatation bestäms av egenskaper som är inneboende i talet 4+3i, som, som framgår av figuren nedan, befinner sig fem enheter från origo (r = 5) och bildar en vinkel på 36,9 grader med den horisontella axeln (φ = 36,9°). Dessa mått används i det som kallas den polära formen av ett komplext tal (reiφ) i motsats till den normala rektangulära formen (a+bi).

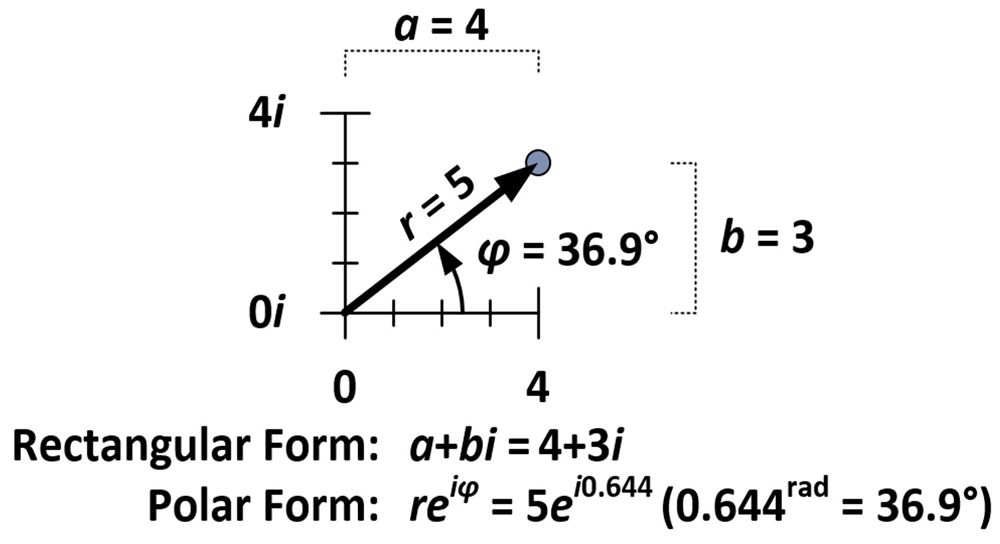
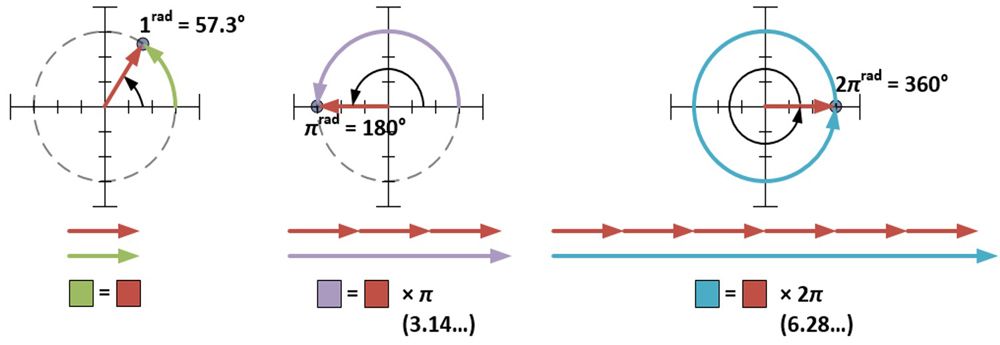
Den polära formen kräver att φ mäts i radianer. En radian (1rad) är ungefär 57,3 grader; det är måttet på den vinkel som bildas när en cirkels radie lindas mot cirkelns omkrets. Ett mått på π radianer omsluter halva cirkeln; ett mått på 2π radianer omsluter en hel cirkel.

Vinkelmåttet för 4+3i är 0,644 radianer (36,9° = 0,644rad), vilket innebär att den polära formen av 4+3i är 5ei0,644. Måtten för r och φ kan också bestämmas för var och en av de husformade punkterna, och ett annat sätt att uppnå den utvidgande/roterande effekten av att multiplicera med 4+3i är att multiplicera varje r med fem och lägga till 36,9 grader (eller 0,644rad) till varje φ. Av denna demonstration ser vi att när komplexa tal multipliceras med varandra multipliceras avstånden och vinklarna adderas. Detta beror på en egenskap som är inneboende i exponenter och som kan visas algebraiskt.

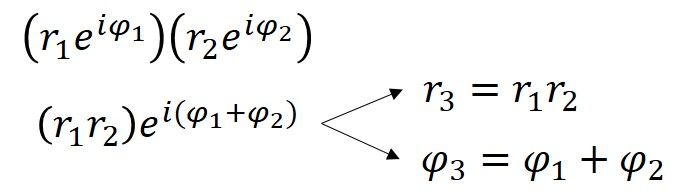
Med polarformen för komplexa tal fastställd är frågan om Eulers identitet bara ett specialfall av a+bi för a = -1 och b = 0. För polarformen reiφ gör detta följaktligen att r = 1 och φ = π (eftersom πrad = 180°).

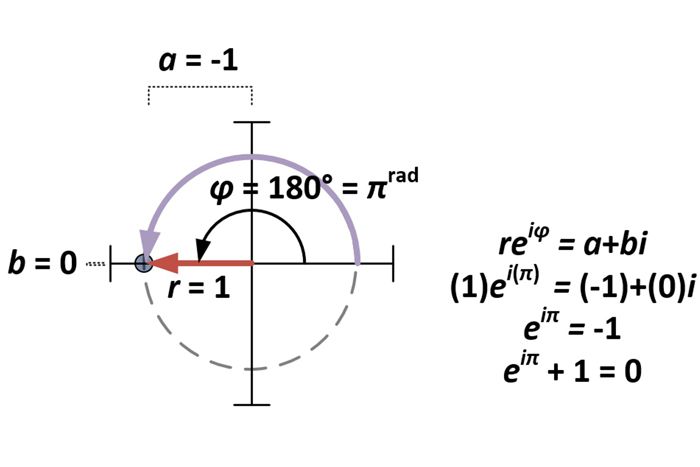
Herledning av polarformen

Trots att Eulers identitet följer av polarformen för komplexa tal är det omöjligt att härleda polarformen (särskilt talets e:s spontana uppkomst) utan att räkna.

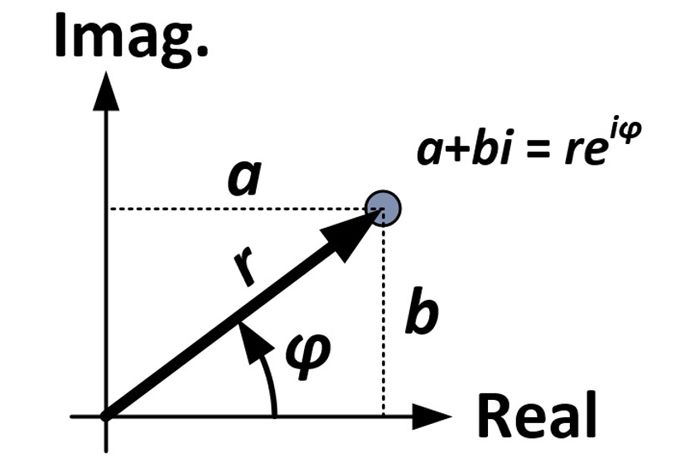
Vi börjar med den rektangulära formen av ett komplext tal:

a + bi

Utifrån diagrammet och trigonometrin kan vi göra följande utbyten:

(r-cosφ) + (r-sinφ)i

Från detta kan vi faktorisera ut r:

r-(cosφ + i-sinφ)

Omedelbart benämns ”cosφ + i-sinφ” cisφ, vilket är en förkortning för ”cosinus plus imaginär sinus”.”

r-cisφ

Funktionen cisφ visar sig vara lika med eiφ. Detta är den del som är omöjlig att visa utan kalkyl. Två härledningar visas nedan:

Därmed skrivs ekvationen r-cisφ i den polära standardformen r-eiφ.