A identidade de Euler é uma igualdade encontrada na matemática que foi comparada a um soneto shakespeariano e descrita como “a mais bela equação”. É um caso especial de uma equação fundacional em aritmética complexa chamada Fórmula de Euler, que o falecido grande físico Richard Feynman chamou em suas palestras de “nossa jóia” e “a fórmula mais notável em matemática”.
Numa entrevista com a BBC, o Prof. David Percy do Instituto de Matemática e suas Aplicações disse que a Identidade de Euler era “um verdadeiro clássico e você não pode fazer melhor que isso … É simples de olhar e, no entanto, incrivelmente profunda, ela compreende as cinco constantes matemáticas mais importantes.”
A Identidade de Euler é escrita simplesmente como: eiπ + 1 = 0
As cinco constantes são:
- O número 0.
- O número 1.
- O número π, um número irracional (com dígitos intermináveis) que é a razão entre a circunferência de um círculo e o seu diâmetro. É aproximadamente 3,14159…
- O número e, também um número irracional. É a base dos logaritmos naturais que surge naturalmente através do estudo do interesse composto e do cálculo. O número e permeia a matemática, aparecendo aparentemente do nada em um vasto número de equações importantes. É aproximadamente 2,71828….
- O número i, definido como a raiz quadrada de um negativo: √(-1). O mais fundamental dos números imaginários, assim chamados porque, na realidade, nenhum número pode ser multiplicado por si mesmo para produzir um número negativo (e, portanto, os números negativos não têm raízes quadradas reais). Mas, em matemática, há muitas situações em que se é obrigado a tomar a raiz quadrada de um negativo. A letra i é portanto usada como uma espécie de stand-in para marcar lugares onde isto foi feito.
Matemático prolífico
Leonhard Euler foi um matemático nascido na Suíça no século XVIII que desenvolveu muitos conceitos que são parte integrante da matemática moderna. Ele passou a maior parte da sua carreira em São Petersburgo, Rússia. Ele foi um dos matemáticos mais prolíficos de todos os tempos, de acordo com a Academia Naval dos EUA (USNA), com 886 trabalhos e livros publicados. Grande parte de sua produção veio durante as duas últimas décadas de sua vida, quando ele era totalmente cego. Houve tanto trabalho que a Academia de São Petersburgo continuou publicando seu trabalho postumamente por mais de 30 anos.
As importantes contribuições de Euler incluem a Fórmula de Euler e o Teorema de Euler, ambos podem significar coisas diferentes, dependendo do contexto. Segundo a USNA, na mecânica, existem “ângulos de Euler (para especificar a orientação de um corpo rígido), o teorema de Euler (que cada rotação tem um eixo), as equações de Euler para o movimento de fluidos e a equação de Euler-Lagrange (que vem do cálculo de variações).”
Multiplicando números complexos
A Identidade de Euler decorre naturalmente das interacções de números complexos que são números compostos por duas peças: um número real e um número imaginário; um exemplo é 4+3i. Os números complexos aparecem numa multiplicidade de aplicações como a mecânica das ondas (um estudo dentro da mecânica quântica) e o desenho de circuitos que utilizam corrente alternada (uma prática comum na engenharia eléctrica). Além disso, números complexos (e seus primos, os números hiper complexos) têm uma propriedade que os torna especialmente úteis para o estudo da computação gráfica, robótica, navegação, dinâmica de vôo e mecânica orbital: multiplicá-los juntos faz com que eles girem. Esta propriedade nos ajudará a entender o raciocínio por trás da Identidade de Euler.
No exemplo abaixo, cinco números complexos são traçados no plano complexo e juntos formam uma “forma de casa”. O plano complexo é similar a uma linha numérica, exceto que é bidimensional. A direção horizontal representa os números reais e o eixo vertical representa números imaginários. Cada número complexo em forma de casa é multiplicado pelo número complexo 4+3i e replotado (seta verde).
Como pode ser visto, multiplicando por 4+3i resulta na forma da casa dilatando (aumentando em área e afastando-se da origem 0+0i pela mesma quantidade) e girando (ficando inclinado por algum ângulo). Para mostrar isto é precisamente o efeito de multiplicar por 4+3i, o efeito de fazer zoom na casa cinco vezes e girar por 36,9 graus também é mostrado (seta vermelha). O mesmo efeito é produzido.
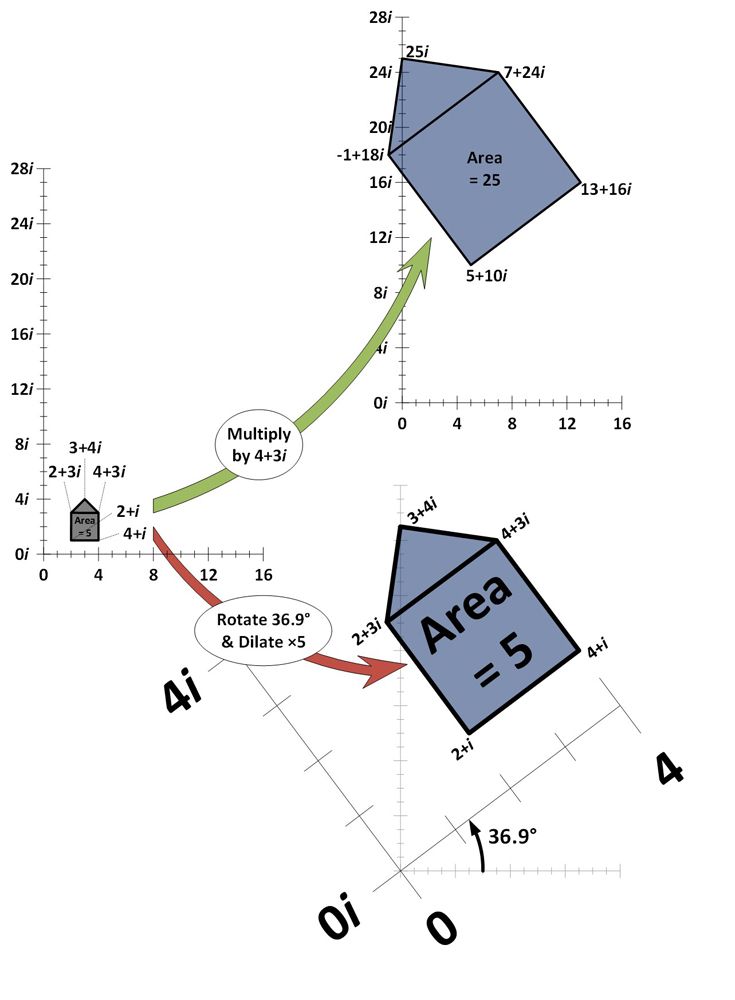
Diferentes quantidades de dilatação e rotação podem produzir os efeitos da multiplicação por qualquer número no plano complexo.
Forma polar de números complexos
A quantidade de rotação e dilatação é determinada por propriedades intrínsecas ao número 4+3i, que, como visto na figura abaixo, é de cinco unidades da origem (r = 5) e forma um ângulo de 36,9 graus com o eixo horizontal (φ = 36,9°). Estas medidas são usadas no que é conhecido como a forma polar de um número complexo (reiφ) em oposição à forma rectangular normal (a+bi).
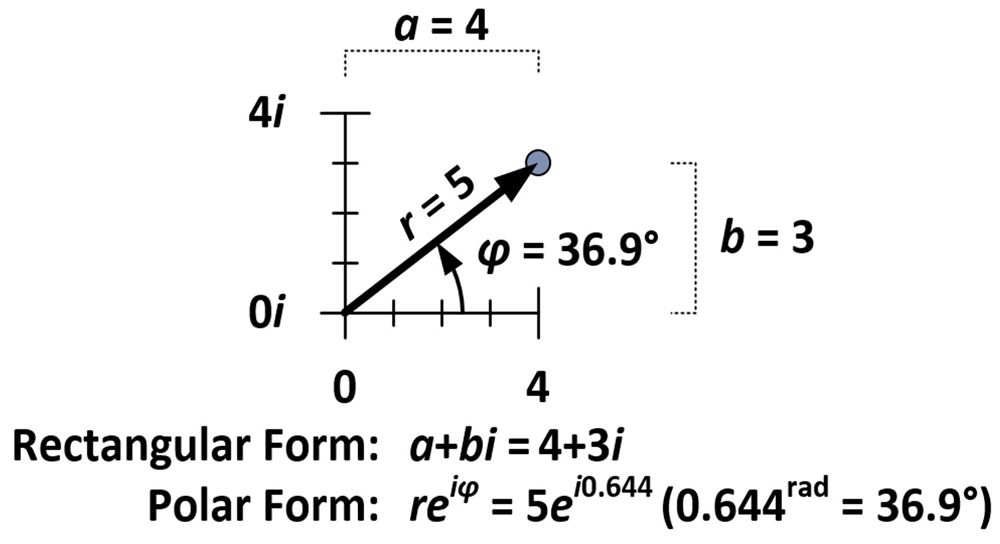
A forma polar requer que φ seja medida em radianos. Um radiano (1rad) é aproximadamente 57,3 graus; é a medida de ângulo feita quando o raio de um círculo é enrolado contra a circunferência desse círculo. Uma medida de π radianos envolve a metade de um círculo; uma medida de 2π radianos envolve um círculo completo.
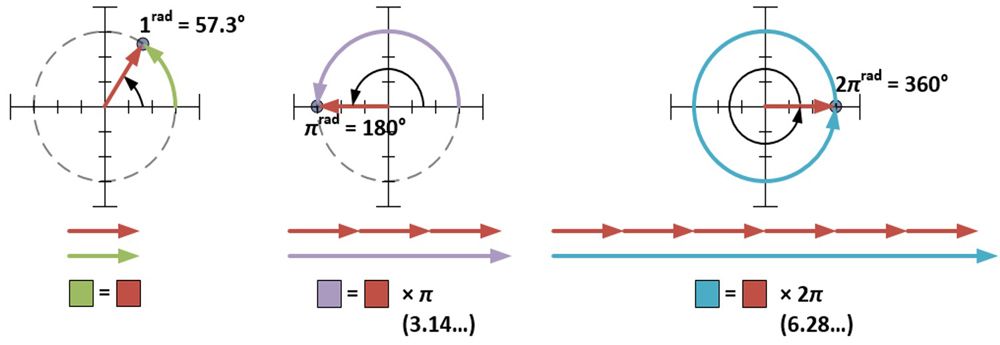
A medida do ângulo para 4+3i é de 0,644 radianos (36,9° = 0,644rad) significando que a forma polar de 4+3i é 5ei0,644. As medidas para r e φ também podem ser determinadas para cada um dos pontos em forma de casa, e ainda outra forma de alcançar o efeito dilatador/rotante da multiplicação por 4+3i é multiplicar cada r por cinco, e adicionar 36,9 graus (ou 0,644rad) a cada φ. A partir desta demonstração, vemos que quando números complexos são multiplicados juntos, as distâncias se multiplicam e os ângulos se somam. Isto é devido a uma propriedade intrínseca aos expoentes, que pode ser mostrada algébricamente.
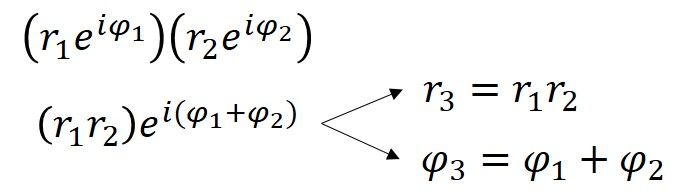
Com a forma polar de números complexos estabelecida, a questão da Identidade de Euler é apenas um caso especial de a+bi para a = -1 e b = 0. Consequentemente, para a forma polar reiφ, isto faz r= 1 e φ = π (desde πrad = 180°).
Derivação da forma polar
Pois a Identidade de Euler segue da forma polar de números complexos, é impossível derivar a forma polar (em particular a aparência espontânea do número e) sem cálculo.
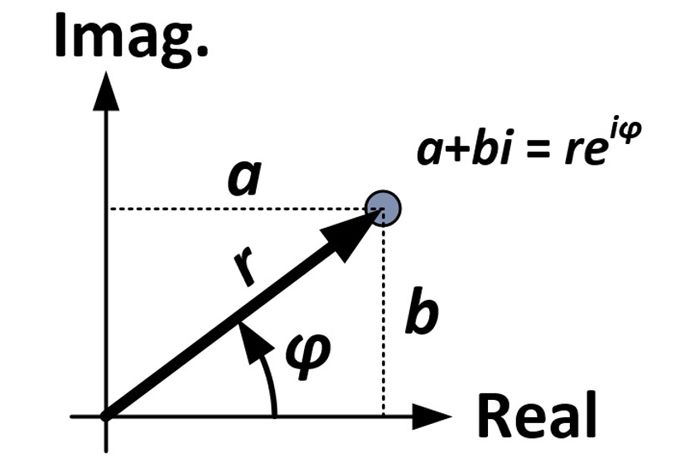
Comecemos com a forma retangular de um número complexo:
a + bi
Do diagrama e trigonometria, podemos fazer as seguintes substituições:
(r-cosφ) + (r-sinφ)i
A partir daqui podemos factorar r:
r-(cosφ + i-sinφ)
Algumas vezes “cosφ + i-sinφ” é chamado cisφ, que é a abreviatura de “cosine plus imaginary sine”.”
r-cisφ
A função cisφ acaba por ser igual a eiφ. Esta é a parte que é impossível de mostrar sem cálculo. Duas derivações são mostradas abaixo:

Assim, a equação r-cisφ é escrita na forma polar padrão r-eiφ.