Tegyük fel, hogy egy gépi tanulási modellt tervezünk. Egy modell akkor mondható jó gépi tanulási modellnek, ha a problématartomány bármely új bemeneti adatát megfelelő módon általánosítja. Ez segít előrejelzéseket tenni a jövőbeni adatokra, amelyeket a modell még soha nem látott.
Tegyük fel, hogy ellenőrizni akarjuk, mennyire jól tanul és általánosít a gépi tanulási modellünk az új adatokra. Ehhez van túlillesztés és alulillesztés, amelyek nagyrészt felelősek a gépi tanulási algoritmusok gyenge teljesítményéért.
Mielőtt tovább merülnénk, értsük meg két fontos fogalmat:
Bias – A modell által tett feltételezések, hogy egy függvényt könnyebben megtanuljon.
Variancia – Ha az adatokat tréningadatokon képezzük és nagyon alacsony hibát kapunk, az adatok megváltoztatásakor, majd ugyanannak a korábbi modellnek a képzésekor magas hibát tapasztalunk, ez a variancia.
Az alulillesztés:
Egy statisztikai modellről vagy egy gépi tanulási algoritmusról akkor beszélünk alulillesztésről, ha nem képes megragadni az adatok mögöttes trendjét. (Ez olyan, mintha alulméretezett nadrágot próbálnánk ráilleszteni!) Az alulillesztés tönkreteszi a gépi tanulási modellünk pontosságát. Előfordulása egyszerűen azt jelenti, hogy a modellünk vagy az algoritmus nem illeszkedik elég jól az adatokhoz. Általában akkor fordul elő, amikor kevesebb adatunk van egy pontos modell felépítéséhez, és akkor is, amikor nem lineáris adatokkal próbálunk lineáris modellt építeni. Ilyen esetekben a gépi tanulási modell szabályai túl egyszerűek és rugalmasak ahhoz, hogy ilyen minimális adatokon alkalmazhatók legyenek, ezért a modell valószínűleg sok téves előrejelzést fog adni. Az alulilleszkedés elkerülhető több adat felhasználásával, valamint a jellemzők szelektálásával történő csökkentésével.
Az alulilleszkedés röviden: Alulilleszkedés – Nagy torzítás és alacsony variancia
Az alulilleszkedés csökkentésének technikái :
1. Növeljük a modell komplexitását
2. Növeljük a jellemzők számát, feature engineeringet végezve
3. Távolítsuk el a zajt az adatokból.
4. Növeljük az epochák számát vagy növeljük a képzés időtartamát, hogy jobb eredményeket kapjunk.
Túlillesztés:
A statisztikai modellről azt mondjuk, hogy túlillesztett, ha sok adattal képezzük (mintha túlméretezett nadrágba illesztenénk magunkat!). Ha egy modellt ennyi adattal képezünk ki, akkor az elkezd tanulni az adathalmazunkban lévő zajból és pontatlan adatbejegyzésekből. Ekkor a modell a túl sok részlet és zaj miatt nem kategorizálja helyesen az adatokat. A túlillesztés okai a nem parametrikus és nem lineáris módszerek, mert az ilyen típusú gépi tanulási algoritmusoknak nagyobb szabadságuk van a modell felépítésében az adathalmaz alapján, és ezért valóban irreális modelleket tudnak építeni. A megoldás a túlillesztés elkerülésére a lineáris algoritmus használata, ha lineáris adataink vannak, vagy a paraméterek, például a maximális mélység használata, ha döntési fákat használunk.
A túlillesztés dióhéjban – Nagy variancia és alacsony torzítás
Példák:
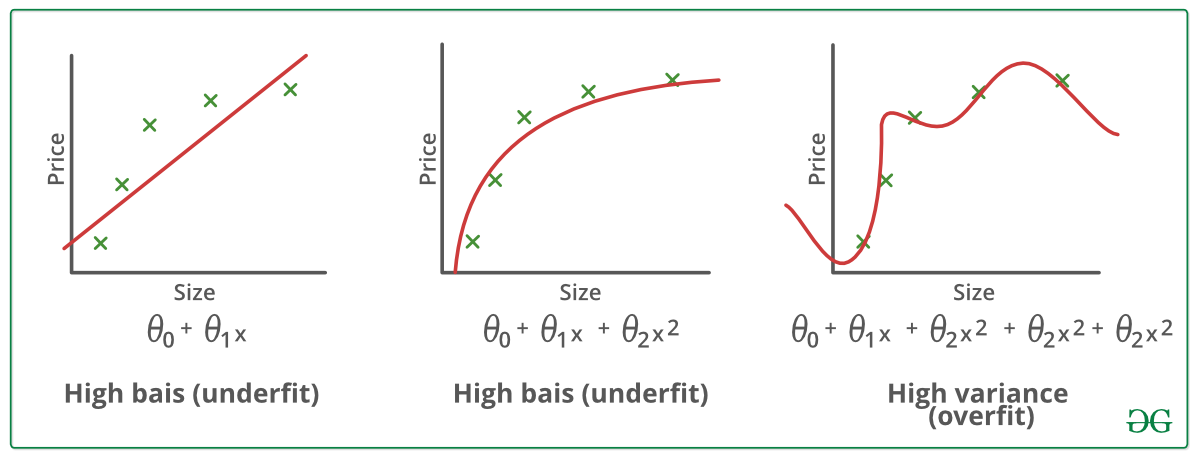
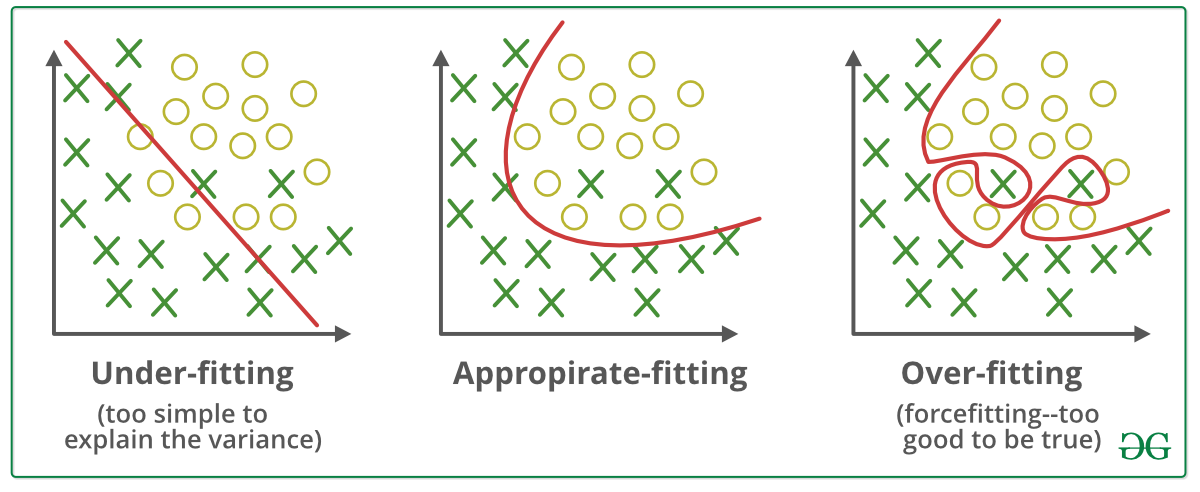
Technikák a túlillesztés csökkentésére :
1. A képzési adatok növelése.
2. A modell összetettségének csökkentése.
3. Korai leállítás a képzési fázisban (tartsuk szemmel a veszteséget a képzési időszak alatt, amint a veszteség növekedni kezd, állítsuk le a képzést).
4. Ridge regularizáció és Lasso regularizáció
5. Ridge regularizáció és Lasso regularizáció
5. A modell összetettségének csökkentése. Kiesés alkalmazása a neurális hálózatoknál a túlillesztés leküzdésére.
Jó illeszkedés egy statisztikai modellben:
Az az eset, amikor a modell 0 hibával teszi a jóslatokat, jó illeszkedésnek mondható az adatokra. Ez az állapot a túlillesztés és az alulillesztés közötti ponton érhető el. Ennek megértéséhez meg kell vizsgálnunk a modellünk teljesítményét az idő múlásával, miközben a modell a képzési adathalmazból tanul.
Az idő múlásával a modellünk folyamatosan tanulni fog, és így a modell hibája a képzési és tesztelési adatokon folyamatosan csökkenni fog. Ha túl sokáig fog tanulni, a modell hajlamosabb lesz a túlillesztésre a zaj és a kevésbé hasznos részletek jelenléte miatt. Ezért a modellünk teljesítménye csökkenni fog. Annak érdekében, hogy jó illeszkedést érjünk el, megállunk egy ponton, közvetlenül azelőtt, hogy a hiba növekedni kezd. Ezen a ponton a modellről azt mondjuk, hogy jó képességekkel rendelkezik a képzési adathalmazokon, valamint a nem látott tesztelési adathalmazunkon.